지역 특징 검출, Local Feature Detection

1. 대응점 찾기

같은 장면을 다른 시점에서 찍은 두 영상의 대응점 쌍 찾기
→ 파노라마, 물체 인식/추적, 스테레오 등
3 단계로 해결
1. 검출(detection): 영상에서 특징점 위치 찾기
2. 기술(description): 특징점 주변 영역을 벡터로 표현
3. 매칭(matching): 두 영상의 특징 벡터 비교 후 대응점 탐색

2. 지역 특징

목표: 시점·스케일·조명 변화에도 견고한 키포인트+디스크립터로 영상 간 대응점을 잡아 정합/추정(호모그래피, F) 에 사용.
- 에지: 에지 강도와 방향 정보만 가지므로 매칭 참여 X
- 코너: 에지 토막에서 곡률이 큰 지점
특징: (위치, 스케일, 방향, 특징 벡터) = $((y, x), s, \theta, v)$로 표현
- 검출: 위치와 스케일
- 기술: 방향과 특징 벡터
요구 성질:
- 반복성: 동일한 물체가 다른 시점, 회전, 조명에서 촬영되어도 검출 가능해야 함
- 분별력: 다른 지점과 혼동되지 않도록 충분히 구별 가능한 패턴이어야 함
- 지역성: 주변 정보에만 의존해 가림(occlusion)이나 배경 변화에 영향을 받지 않아야 함
- 정확성: 위치 및 스케일 계산이 정확해야 함
- 적당량: 너무 많지도 적지도 않게 검출되어야 함
- 계산 효율: 연산 속도가 빠르고 실시간 적용 가능해야 함
지역 특징 검출 원리
- 인지 실험: 사람에게 쉬운 곳이 컴퓨터에게도 쉽다
- 여러 방향으로 밝기 변화가 나타나는 곳 → 높은 점수

3. Corner Detection

작은 윈도우를 여러 방향으로 조금씩 이동했을 때 모든 방향에서 밝기 변화가 크면 코너, 한 방향만 크면 에지, 전반적으로 작으면 평탄 영역

방법	핵심 측정	장점	한계/주석
모라벡	이산 방향 SSD의 최소값	간단·빠름	1픽셀/소수 방향, 노이즈 취약
해리스	$\begin{align} R &= \det(M) \alpha \mathrm{trace}^2 = \lambda_1 \lambda_2 - k(\lambda_1 + \lambda_2)^2 \end{align}$	고유값 해석 기반, 견고	$\alpha$·윈도우 설정 필요, 스케일 불변 아님
헤시안 행렬식	$\det(H)=I_{xx}I_{yy}-I_{xy}^2$	교차/첨두 구조 검출	2차 미분의 노이즈 민감성, 스케일 의존
LoG	$\nabla^2(G*I)$	스무딩+2차미분 일관, 블롭 강함	스케일 고정 시 한계 → 스케일 공간 필요
SUSAN	USAN 크기	비미분·노이즈 견고	임계 $t$ 민감, 질감 많은 영역 과검출 가능

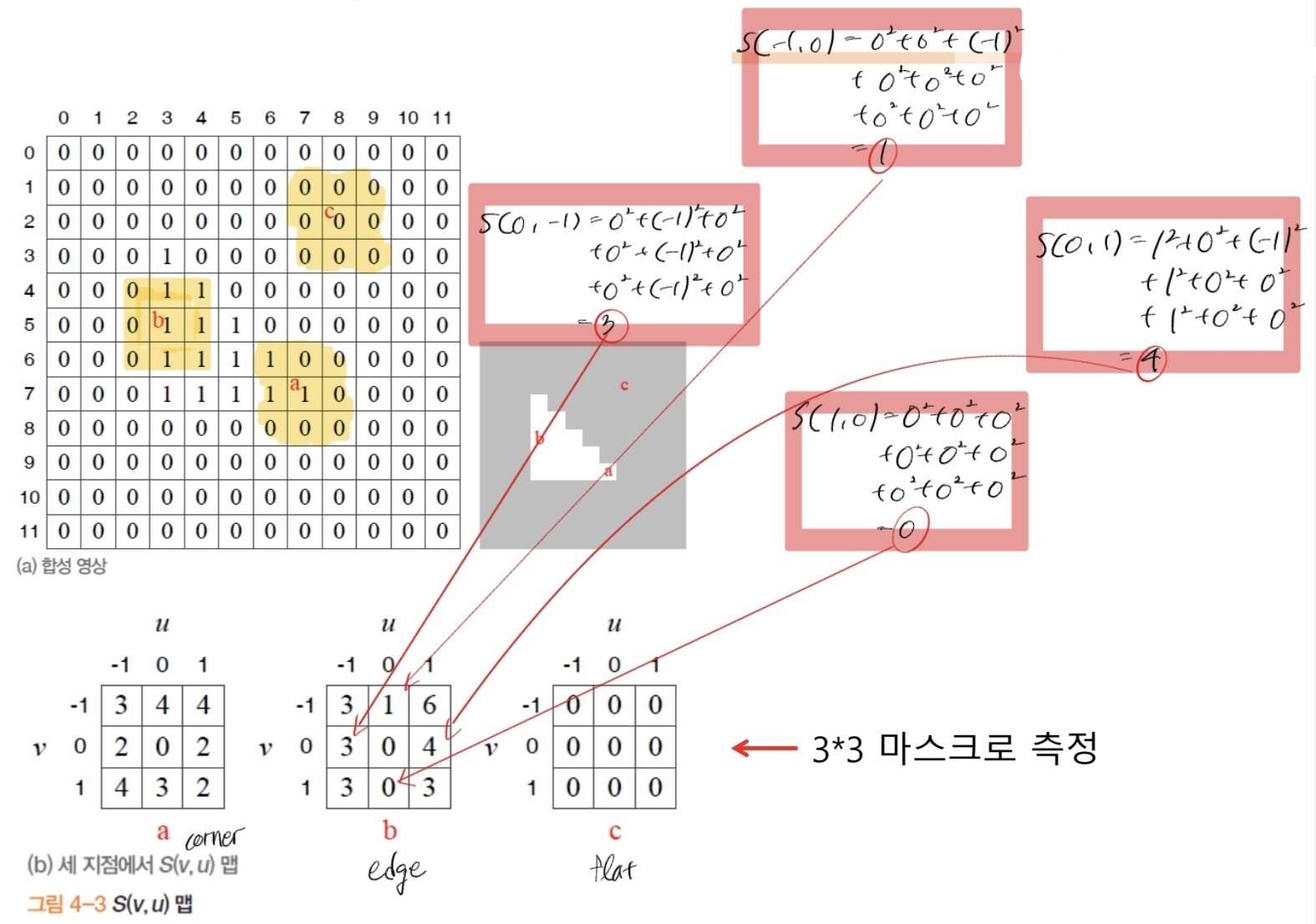
3.1. 모라벡(Moravec) 알고리즘

측정 원리: 정사각 윈도우(예: 3×3, 9×9)를 기준점에서 이웃 방향으로 한 화소씩 평행이동하여, SSD(제곱차합) 변화를 계산.
수식: $S(u,v)=\sum _y \sum _x w(y, x)(f(y+v, x+u) - f(y, x))^2$
특징 가능성 값 $C$:
- \[C = min(S(0, 1), \, S(0, -1), \, S(1, 0), \, S(-1, 0)) ≥ T\]
예제
한계:
- 한 화소 이동 + 4개(또는 8개) 이산 방향만 고려 → 방향성 편향
- 잡음 대책 부재

3.2. 해리스(Harris) 코너

유도(개요):
- 가중치 제곱차합: $S(u,v)=\sum _y \sum _x G(y, x)(f(y+v, x+u) - f(y, x))^2$
- 1차 테일러 전개로 근사:
  - 테일러 확장 $f(y+v, x+u) \cong f(y, x) + vd_y(y, x) + ud_x(y, x)$을 대입
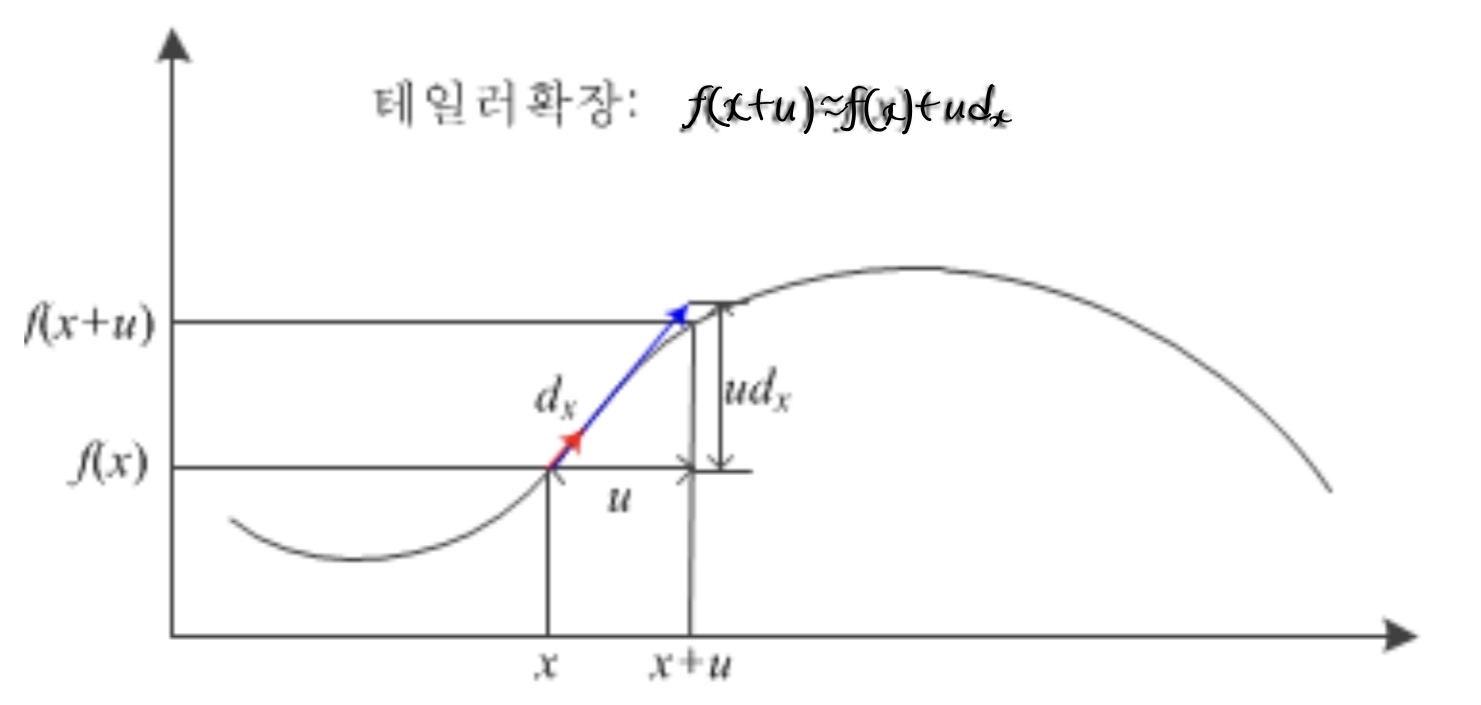
  - \[S(u,v)=\sum _y \sum _x G(y, x)(vd_y(y, x) + ud_x(y, x))^2\]
- 2차 모멘트 행렬(=구조 텐서) $M$ 도출
  - \[\begin{align} S(u, v) & \cong \sum_y \sum_x G(y, x)(vd_y + ud_x)^2 \\ & = \sum_y \sum_x G(y, x)(v^2d_y^2 + 2vud_yd_x + u^2d_x^2) \\ & = \sum_y \sum_x G(y, x)(v \; u) \begin{pmatrix} d_y^2 & d_yd_x \\ d_yd_x & d_x^2 \\\end{pmatrix} \begin{pmatrix} v \\ u \\\end{pmatrix} \\ & = (v \; u) \sum_y \sum_x G(y, x) \begin{pmatrix} d_y^2 & d_yd_x \\ d_yd_x & d_x^2 \\\end{pmatrix} \begin{pmatrix} v \\ u \\\end{pmatrix} \end{align}\]
  - $d_y^2$: y축 방향
  - $d_x^2$: x축 방향
  - $d_yd_x$: 방향 벡터.
- 이를 분석해 코너 판정.
고유값 해석: $M$의 고유값 $\lambda_1,\lambda_2$
- 둘 다 작음 → 평탄
- 하나만 큼 → 에지
- 둘 다 큼 → 코너.
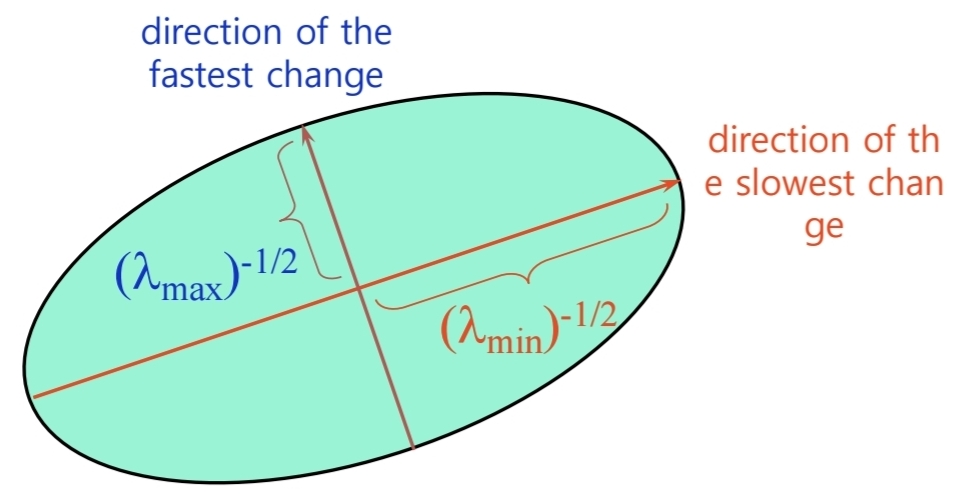
기하적 해석(타원 등고선)
- $E(u,v)=c$는 타원이고, 주축 방향이 $e_1,e_2$, 축 길이는 $1/\sqrt{\lambda_1},\,1/\sqrt{\lambda_2}$.
- $λ$ 클수록 그 축은 짧음(그 방향으로 조금만 움직여도 변화 큼).
응답식:
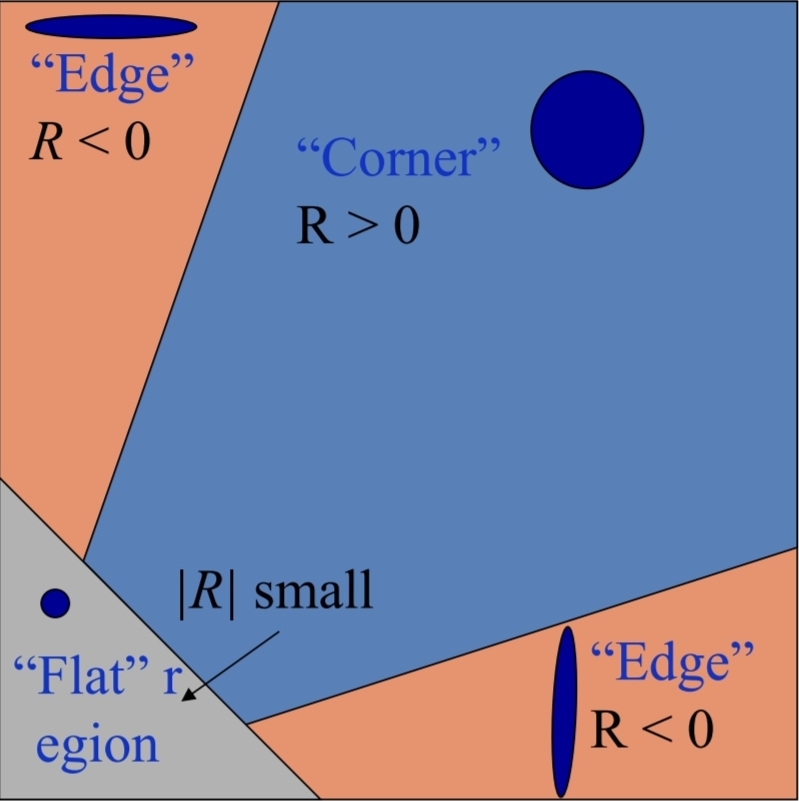
- \[R=\det(M)-\alpha\mathrm{trace}(M)^2 = \lambda_1 \lambda_2 - k(\lambda_1 + \lambda_2)^2,\quad \alpha\approx0.04\sim0.06\]
  - $R>0$이면 코너
  - $R<0$이면 에지
  - $\vert R \vert$ 작으면 평탄
- 고유값 계산 회피 → 속도 향상
  - \[A = \begin{pmatrix} p & r \\ r & q \end{pmatrix}\]
  - $C = (pq-r)^2 - k(p+q)^2$
예제
검출 절차:
- 가우시안 미분으로 기울기
- 가우시안 윈도우에서 $M$ 계산
- $R$ 계산
- 임계값(threshold)
- 비최대 억제(NMS).
장점: 회전 불변성, 노이즈에 강함, 계산 효율성
단점: 스케일 불변성 X, 조명 변화에 민감, 고정 윈도우 크기

3.3. 헤시안 행렬식(Hessian determinant)

핵심: 2차 미분으로 곡률을 직접 평가. 가우시안 포함 헤시안 $H_\sigma$ 사용(노이즈 완화).
지표: $C = \det(H)=I_{xx}I_{yy}-I_{xy}^2$
특징: 에지보다 교차/첨두 구조에 강함. 가우시안 스무딩 후 2차 미분을 쓰는 맥락을 7장(미분 전 스무딩)과 연결해 이해.

3.4. LoG (Laplacian of Gaussian)

정의: 스무딩(가우시안) 뒤 라플라시안(2차 미분) 으로 블롭/코너성 응답을 얻음(스케일마다 응답 극값/영교차 활용)
- \[\mathrm{LoG}_\sigma = \nabla^2 (G_\sigma * I) = (\nabla^2 G_\sigma) * I\]
- 미분 전 스무딩 우선(노이즈 증폭 억제).
지표: $C = \nabla^2 = \text{trace}(H) = d_{yy}(\sigma) + d_{xx}(\sigma)$
특징: 스케일 변화에도 대응 가능

3.5. 슈산(Smallest Uni-value Segment Assimilating Nucleus, SUSAN) 알고리즘

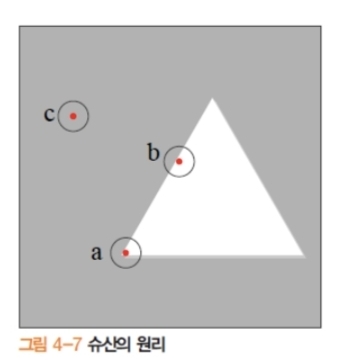
원리: 중심 화소와 이웃 화소 간 밝기 유사도로 USAN(유사 영역) 크기를 계산, USAN이 작을수록 코너성 강함(에지는 중간, 평탄은 큼).
- 파라미터 $t$로 “유사”의 범위를 결정.
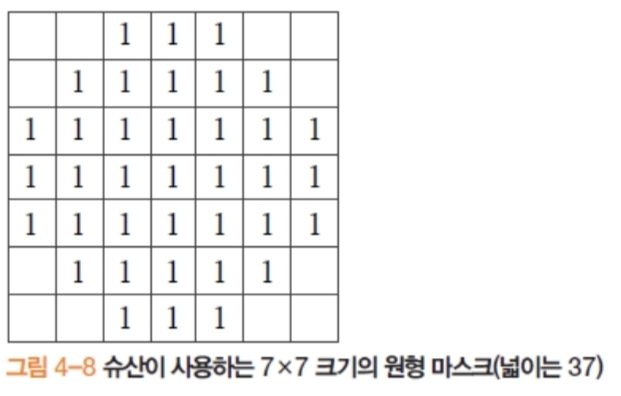
장점(맥락): 미분을 직접 쓰지 않아 노이즈에 비교적 강인, 구조적 변화(코너)에서 USAN이 급감.
수식:
- \[\text {usan \, area}(r_0) = \sum_r s(r, r_0)\]
- \[s(r, r_0) = \begin{cases} {1, \; |f(r) - f(r_0)| \leq t_1} \\ 0, \; \text {if not} \end{cases}\]
- \[C = \begin{cases} q - \text {usan \, area}(r_0), \; \text {usan \, area}(r_0) \leq t_2 \\ 0, \; \text {if not} \end{cases}\]