[COMPUTER VISION] 영상 처리 연산 2
목차
- 기하 연산
- 정의
- 변환 종류와 성질
- 기본(원자) 변환
- 군(그룹)별 변환 체계
- 비선형/국소 변형(Non-rigid, Warping)
- 동차좌표·행렬
- 전방 vs 후방 매핑
- 보간(Interpolation)과 반(反)에일리어싱
- 다해상도
- 알고리즈
- 모폴로지(Morphology)
- 이진 모폴로지 (Binary)
- 명암(그레이스케일) 모폴로지
기하 연산
1. 정의
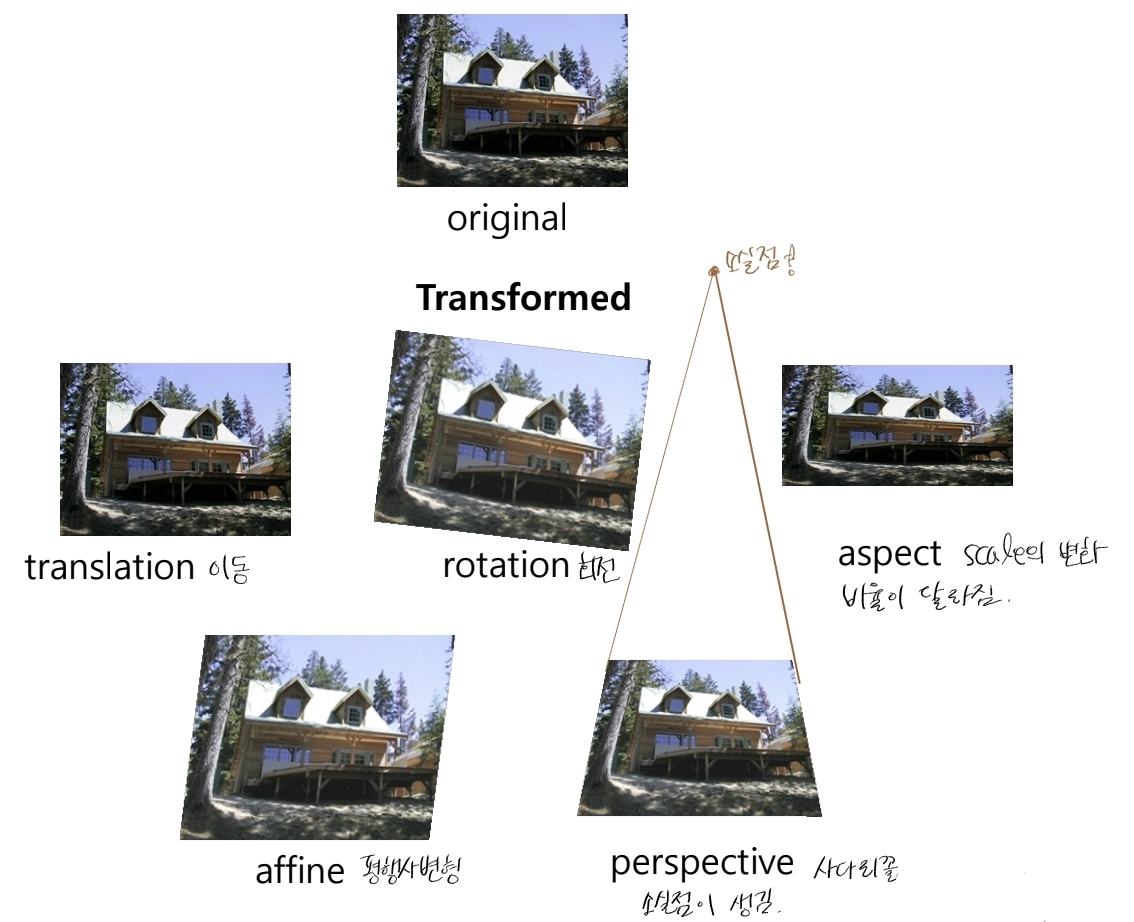
- 일정한 기하 연산으로 결정된 화소 위치의 값을 가져와 새 값을 만든다.
- 좌표를 변환해 어디서 샘플링할지를 정하는 연산이다.
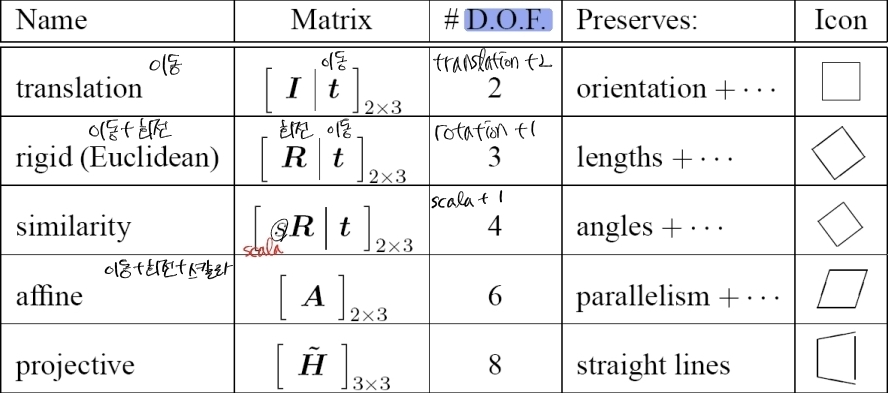
2. 변환 종류와 성질
2.1. 기본(원자) 변환
- 이동(Translation)
-
\[\begin{bmatrix}
x'\\ y'\\ 1
\end{bmatrix}=
\begin{bmatrix}
1 & 0 & t_x\\
0 & 1 & t_y\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x\\ y\\ 1
\end{bmatrix}\]
- 회전(Rotation, 각도 $\theta$)
- 길이·각도 보존(등거리).
-
\[\begin{bmatrix}
x'\\ y'\\ 1
\end{bmatrix}=
\begin{bmatrix}
\cos\theta & -\sin\theta & 0\\
\sin\theta & \cos\theta & 0\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
x\\ y\\ 1
\end{bmatrix}\]
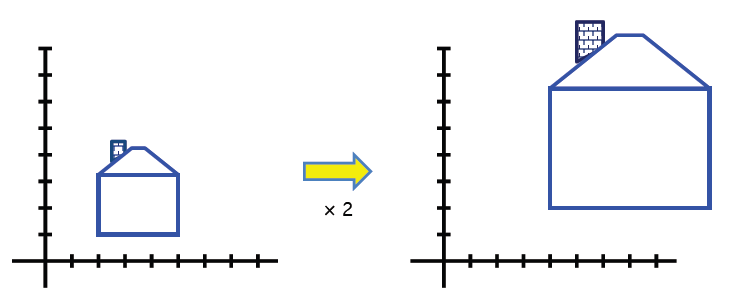
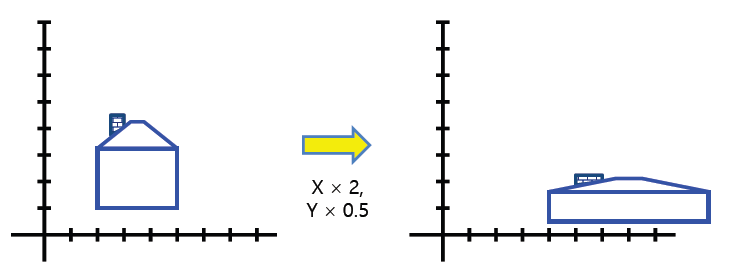
- 스케일(Scaling): 축 방향 길이만 바뀜, 축 혼합 없음.
-
\[\begin{bmatrix}s_x&0&0\\
0&s_y&0\\
0&0&1\end{bmatrix}\]
- Uniform Scale
- Nonuniform Scale
- 시어(Shear/Skew): 회전 × 스케일 × 회전
- 축을 서로 섞는 선형변환(각도 변화), 평행성은 보존하지만 모양이 기울어짐.
-
\[\begin{bmatrix}
1 & k_x & 0\\
k_y & 1 & 0\\
0 & 0 & 1
\end{bmatrix}\]
- 대칭(Reflection): 축에 대해 부호 반전(예: x-축 반사)
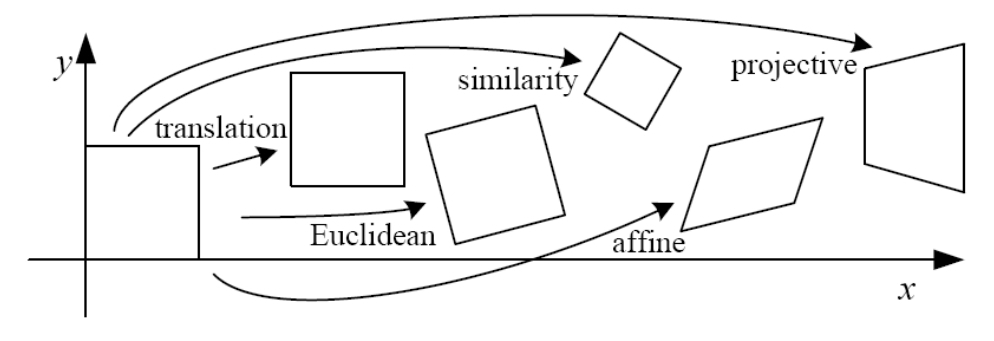
2.2. 군(그룹)별 변환 체계
- 유클리드/강체(Rigid/Euclidean): 회전+이동 (거리·각도 보존, 3 DoF)
- 거리, 각도, 면적(2D) 보존
- 최소 2–3 쌍 대응점(중심 정규화 권장)
-
\[\mathbf{x}'=\mathbf{R}\mathbf{x}+\mathbf{t},\ \mathbf{R}\in SO(2)\]
- 유사(Similarity): Rigid + 등방 스케일(비율 보존, 4 DoF)
- 각도, 비율 보존(거리·면적은 스케일에 따라 변함)
- 최소 2–3 쌍 대응점(중심 정규화 권장)
-
\[\mathbf{x}'=s\mathbf{R}\mathbf{x}+\mathbf{t}\]
- 아핀(Affine): 선성 + 이동(평행성 보존, 6 DoF)
- 직선·평행성·면적 비율 보존(각도·길이 불변 아님)
- 최소 3 쌍(6방정식)
-
\[\begin{bmatrix}
x'\\ y'\\ 1
\end{bmatrix} = \underbrace{\begin{bmatrix}
a_{11 } &a_{12} & t_x\\
a_{21} & a_{22} & t_y\\
0 & 0 & 1
\end{bmatrix}}_{\text{2×3 추정 시 자주 사용}}
\begin{bmatrix}
x\\ y\\ 1
\end{bmatrix}\]
- 투영/사영(Projective, Homography): 직선 보존(평행성은 불보존, 8 DoF)
- 직선만 보존(평행성·길이·각도 불변 아님)
- 최소 4 쌍(8방정식)
-
\[\begin{bmatrix}
x'\\ y'\\ w'
\end{bmatrix} = \underbrace{\begin{bmatrix}
h_{11}&h_{12}&h_{13}\\
h_{21}&h_{22}&h_{23}\\
h_{31}&h_{32}&1\end{bmatrix}}_{\mathbf{H}}
\begin{bmatrix}
x \\ y \\ 1
\end{bmatrix}, \quad (x'/w',y'/w')\]
2.3. 비선형/국소 변형(Non-rigid, Warping)
- 다항(Polynomial) 워프: (x’,y’)를 (x,y)의 다항식으로 모델링(왜곡 보정)
- Thin-Plate Spline(TPS): 소수의 랜드마크로 매끄러운 곡면 변형
- B-spline/Free-Form Deformation(FFD): 격자 제어점으로 국소 변형
- 광류 기반 워프(Optical Flow warp): 픽셀 단위 변위장으로 프레임 정합
3. 동차좌표·행렬
- 동차 좌표: $\dot{x}=(\,y\;\; x\;\; 1\,)$
- 동차행렬: $(x,y)\to(x,y,1)$로 확장하면 2D 변환을 3×3 행렬 하나로 통일적으로 표현·조합 가능.
- e.g. 평행이동 행렬(행-벡터 우측곱 규약): T(3,2)
-
\[\dot{H}=T(3,2)=
\begin{pmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
3 & 2 & 1
\end{pmatrix}\]
-
\[\dot{x}'=(\,y'\;\; x'\;\; 1\,)=
\dot{x}\,\dot{H}=
(\,y\;\; x\;\; 1\,)
\begin{pmatrix}
a_{11} & a_{12} & 0\\
a_{21} & a_{22} & 0\\
a_{31} & a_{32} & 1
\end{pmatrix}\]
-
\[y' = a_{11}y + a_{21}x + a_{31}, \qquad
x' = a_{12}y + a_{22}x + a_{32}\]
- 예제:

- 동차좌표 사용하는 이유: 여러 변환을 곱으로 결합해 한 번에 적용 (계산 효율↑)
4. 전방 vs 후방 매핑
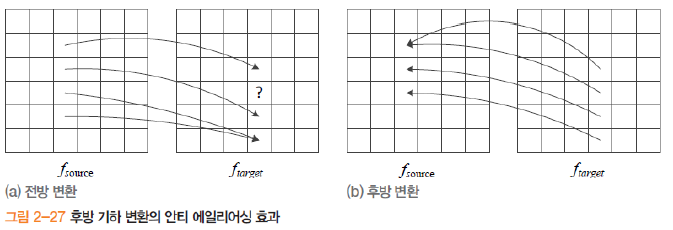
- 전방(forward) 매핑: 원 영상의 픽셀을 변환해 타깃 위치에 찍기
- 후방(backward) 매핑 타깃의 각 픽셀에서 역변환으로 원 영상의 실수 좌표를 찾아 보간
- 역행렬을 미리 구해 두고 후방 매핑으로 샘플링한다
- 안티에일리어싱 효과.
4.1. 알고리즘
- 전방 기하 변환:

- 후방 기하 변환:

5. 보간(Interpolation)과 반(反)에일리어싱
- 왜 보간이 필요한가: 실수 좌표를 정수로 반올림하면 에일리어싱 발생
- 주변 화소로 보간해 완화 → 거리에 대한 비율
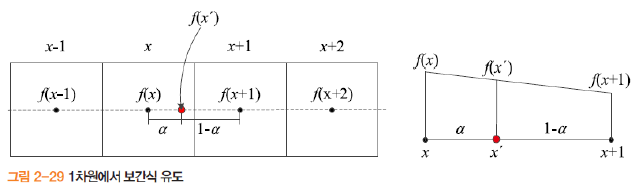
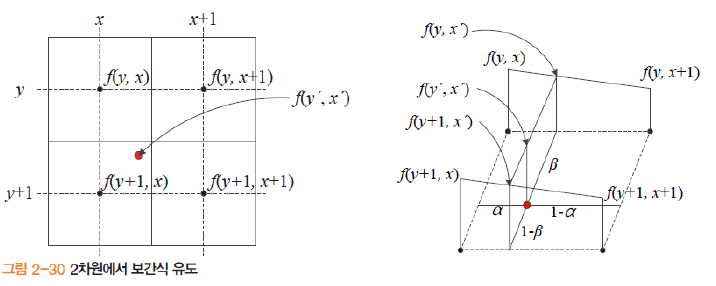
- 보간식
- 1차원 보간식 유도: $f(x’)=(1-\alpha)\,f(x)+\alpha\,f(x+1)$
- 2차원 보간식 유도: \(\begin{aligned}
f(y, x') &= (1-\alpha) f(y,x) + \alpha f(y, x+1),\\
f(y+1, x') &= (1-\alpha) f(y+1,x) + \alpha f(y+1, x+1),\\
f(y', x') &= (1-\beta) f(y, x') + \beta f(y+1, x')
\end{aligned}\)
- 방법과 비교:
- 최근접(nearest): 가장 빠르나 블록/톱니 아티팩트.
- 양선형(bilinear): 4이웃 가중 평균(균형 잡힌 화질/속도)
- 양삼차(bicubic): 16이웃, 부드러움/에지 보존↑(연산량↑).
6. 다해상도
- 해상도를 줄이거나 늘리는 연산
- 다양한 응용
- 멀티미디어 장치에 디스플레이
- 물체 크기 변환에 강인한 인식 등
- 스케일이 다양한 물체 처리 가능
- 업샘플링과 다운샘플링
- 피라미드
- 피라미드 구축 연산식: \(f_k(j,i)
= f_{k-1}\!\left(\frac{j}{r},\,\frac{i}{r}\right),
\qquad r=\frac{1}{2},\; 1\le k \le q\)
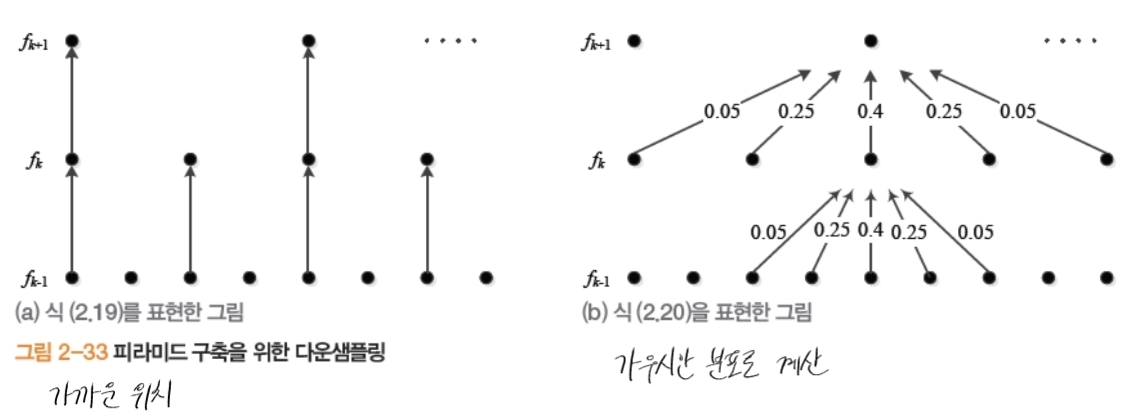
- Burt & Adelson 방법
- 수식: \(f_k(j,i)
= \sum_{y=-2}^{2}\sum_{x=-2}^{2} w(y,x)\;
f_{k-1}\!\left(\frac{j}{r}+y,\; \frac{i}{r}+x\right),
\qquad r=\frac{1}{2},\; 1\le k \le q\)
- 모든 화소가 50%씩 공헌

7. 모폴로지(Morphology)
- 모폴로지: 본래 생물학의 ‘형태 변화’ 개념에서 시작
- 수학적 모폴로지는 영상을 원하는 형태로 바꾸는 규칙적 연산의 집합 → 패턴을 원하는 형태로 변환하는 기법
7.1. 이진 모폴로지 (Binary)
- 대상: 값이 0/1(또는 0/255)인 이진 영상.
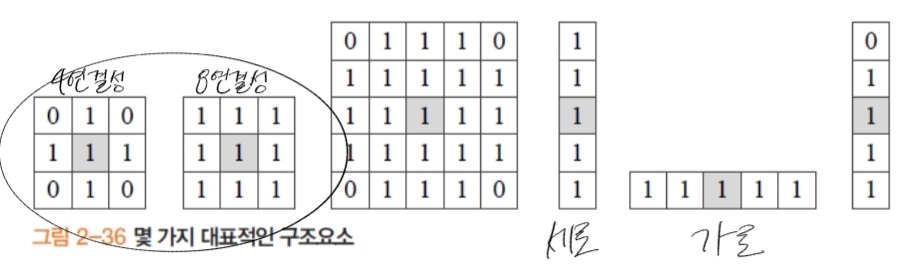
- 구조요소
- 연산
- $S_t={\,s+t \mid s\in S\,}$
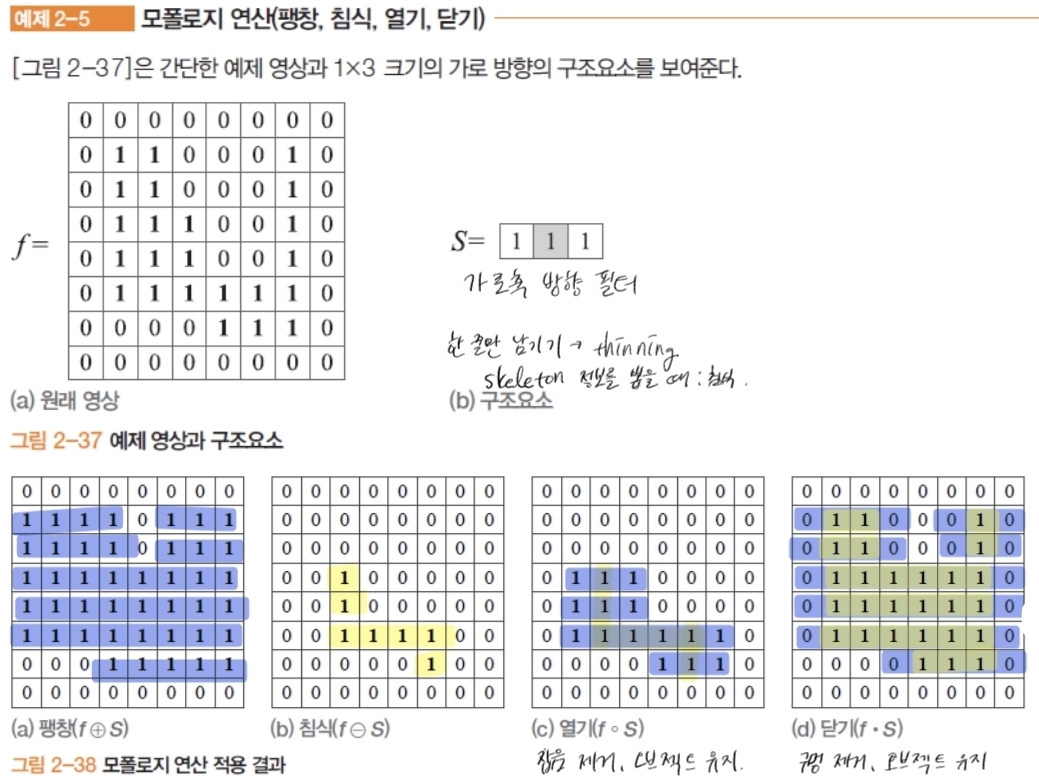
- 팽창: 두꺼워짐/커짐(틈 메움·연결 강화)
- $f\oplus S=\bigcup_{x\in f} S_x$
- 침식: 얇아짐/작아짐(작은 점·돌기 제거에 유리)
- $f\ominus S={\,x \mid x+s\in f,\ \forall s\in S\,}$
- 열기(침식→팽창): 작은 잡음 제거·가느다란 돌기 제거
- $f\circ S=(f\ominus S)\oplus S$
- 닫기(팽창→침식): 작은 구멍 메움·틈새 채움
- $f\bullet S=(f\oplus S)\ominus S$
- 예제
7.2. 명암(그레이스케일) 모폴로지
- 대상: 0–255 등 연속 톤(그레이스케일) 영상.
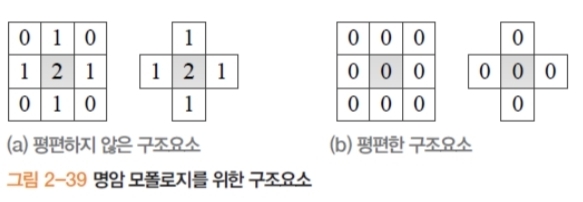
- 구조 요소
- 연산
- 명암 팽창(평편 X 구조요소)
- $(f \oplus S)(j,i)= \max_{(y,x)\in S}\big(f(j-y,i-x)+S(y,x)\big)$
- 명암 침식(평편 X 구조요소)
- $(f \ominus S)(j,i) = \min_{(y,x)\in S}\big(f(j+y,i+x)-S(y,x)\big)$
- 명암 팽창(평편 O 구조요소)
- $(f \oplus S)(j,i) = \max_{(y,x)\in S} f(j-y,i-x)$
- 명암 침식(평편 O 구조요소)
- $(f \ominus S)(j,i) = \min_{(y,x)\in S} f(j+y,i+x)$
- 열기
- $f \circ S = (f \ominus S) \oplus S$
- 닫기
- $f \bullet S = (f \oplus S) \ominus S$
- 명암 모폴로지(특히 closing 등)의 실전 활용 빈도·효익이 낮다










Comments