[COMPUTER VISION] 영상 처리 연산 1
목차
- 영상 처리 연산
- 점 연산(Point operation)
- 영역 연산(Spatial/Neighborhood operation, Filtering)
- 상관(correlation) vs 컨볼루션(convolution)
- 컨볼루션 연산의 대수적 성질
- 대표 필터와 효과
영상 처리 연산
1. 점 연산(Point operation)
- 정의: 한 픽셀의 새 값이 오직 그 픽셀 자신의 명암값만으로 결정되는 변환
-
\[f_{out}(i, j) = t(f_1(i, j), \, f_2(i, j), \, ..., \, f_k(i, j))\]
- 형태
- 선형 점 연산: 밝기·대비 조절 등

-
\[f_{out}(i, j) = t(f(i, j))
= \begin{cases}
min(f(i, j) + a, \, L-1), \quad \text{(밝게)} \\
max(f(i, j) - a, \, 0), \quad \text{(어둡게)} \\
(L-1) - f(i, j), \quad \text{(반전)}
\end{cases}\]
- 비선형 점 연산: 감마 수정(표시 장치 보정 등)

-
\[f_{out}(i, j) = (L-1) \times (\hat f(i, j))^\gamma \quad \text {이때} \; \hat f(i, j) = \frac {f(i, j)}{L-1}\]
- 디졸브(dissolve): 두 영상 섞기(점 연산이지만 (k=2) 입력) e.g. fade in/out

-
\[f_{out}(i, j) = \alpha f_1(i, j) + (1 - \alpha)f_2(i, j)\]
- 특징/용도 요약: 국소 문맥을 보지 않으므로 빠르고 단순, 명암 재매핑(밝기/대비/감마), 영상 간 블렌딩에 효과적.
2. 영역 연산(Spatial/Neighborhood operation, Filtering)
- 정의: 한 픽셀의 새 값이 이웃 화소들의 명암값 함수로 정해짐.
- 무엇에 쓰나?
- 향상(노이즈 감소(denoise), 사이즈 조정(resize), 대조 강화(contrast))
- 정보 추출(texture, edges, keypoints)
- 패턴 검출(템플릿 매칭)
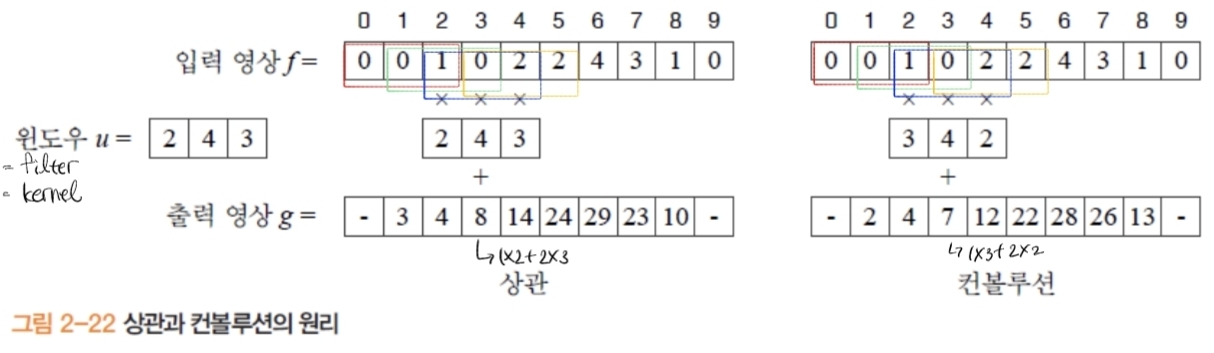
2.1. 상관(correlation) vs 컨볼루션(convolution)
- 상관: “원시적인 매칭 연산(윈도우 형태 템플릿으로 물체 검출)”
- 컨볼루션: 커널을 좌우·상하 뒤집은 후 상관을 적용 → 내가 원하는 윈도우와 동일하게 출력시키기 위해 적용
- “컨볼루션은 커널을 뒤집어 적용, 상관/컨볼루션은 유사도 최대 위치를 찾는 동일한 맥락”.
- 수식
- 상관: \(g(i) = u \otimes f = \sum_{x=-\frac{(w-1)}{2}}^{\frac{(w-1)}{2}} u(x)\,f(i+x)\)
- 컨볼루션: \(g(i) = u \ast f
= \sum_{x=-\frac{(w-1)}{2}}^{\frac{(w-1)}{2}}
u(x)\,f(i-x)\)
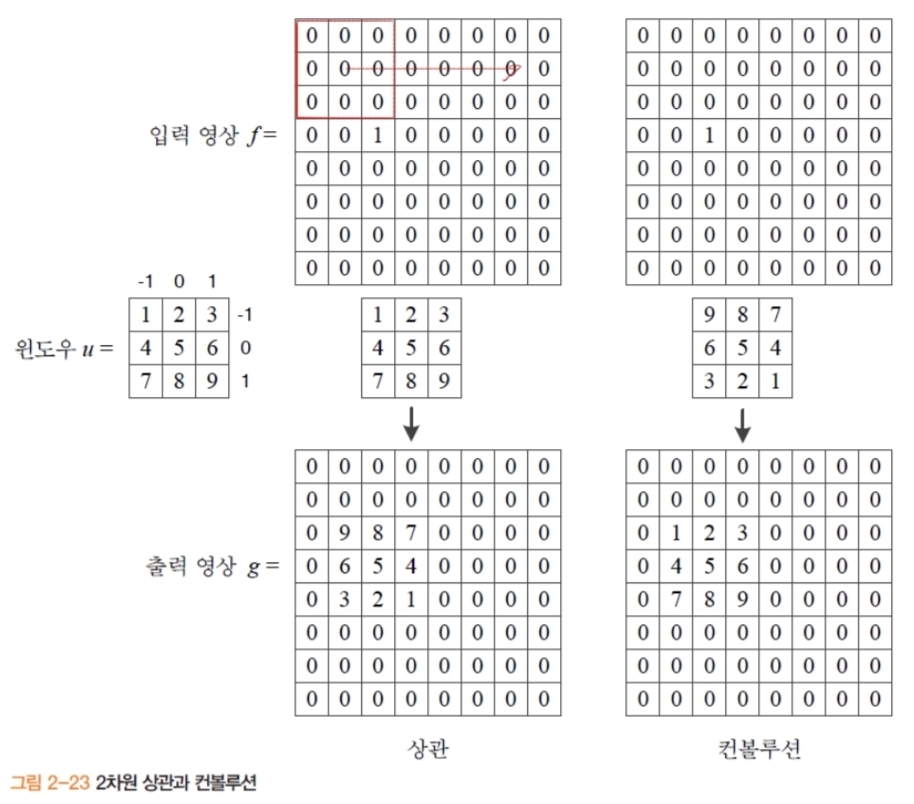
- 수식
- 상관: \(g(j,i) = u \otimes f
= \sum_{y=-\frac{(h-1)}{2}}^{\frac{(h-1)}{2}}
\sum_{x=-\frac{(w-1)}{2}}^{\frac{(w-1)}{2}}
u(y,x)\,f(j+y,i+x)\)
- 컨볼루션: \(g(j,i) = u \ast f
= \sum_{y=-\frac{(h-1)}{2}}^{\frac{(h-1)}{2}}
\sum_{x=-\frac{(w-1)}{2}}^{\frac{(w-1)}{2}}
u(y,x)\,f(j-y,i-x)\)
2.2. 컨볼루션 연산의 대수적 성질
- 선형성: $filter(f_1 + f_2) = filter(f_1) + filter(f_2)$
- 이동 불변성: $filter(shift(f)) = shift(filter(f))$
- 교환 법칙: $a \times b = b \times a$
- 결합 법칙: $a \times (b \times c) = (a \times b) \times c$
- 분배 법칙: $a \times (b + c) = (a \times b) + (a \times c)$
- 스칼라 결합: $ka \times b = a \times kb = k (a \times b)$
- 항등원: $e = [0, 0, 1, 0, 0], a \times e = a$
- 결론: 여러 필터를 연속 적용 ≡ 하나의 등가 필터(성능·설계 단순화).
2.3. 대표 필터와 효과
-
\[h[m, n] = \sum _{k, l} f[m+k, n+l]\]

- Smoothing, 스무딩(저역통과)
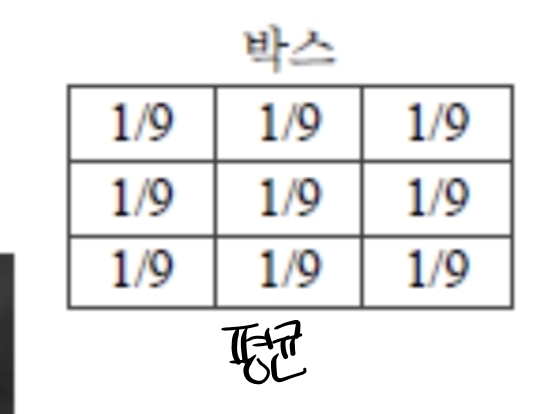
- 박스/가우시안: 노이즈 저감, 부드러워짐.
- 박스 특징: 각 픽셀의 인접 픽셀의 평균값으로 교체, 격자 무늬
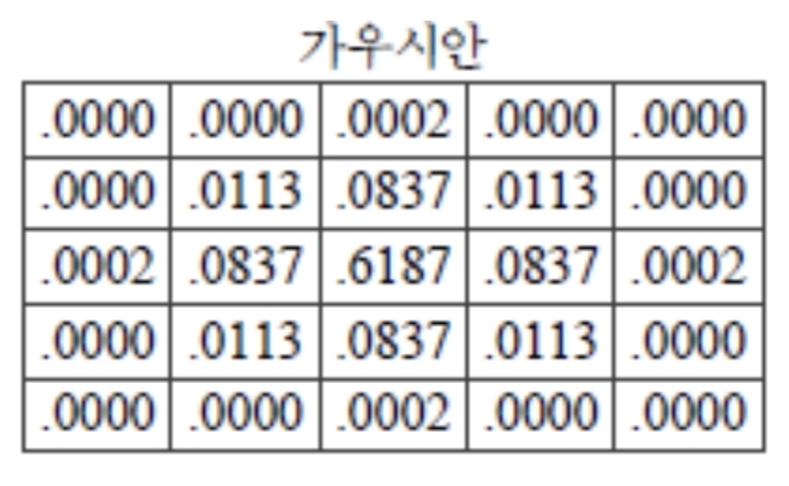
- 가우시안 특징: 고주파 제거, 자기 컨볼루션 → 폭 증가($\sigma !\to! \sigma\sqrt{2}$), 분리 가능(2D = 1D×1D).
- 5×5 가중 커널 예시(중심 가중, 주변 작음).
- Sharpening, 샤프닝(고주파 강조)
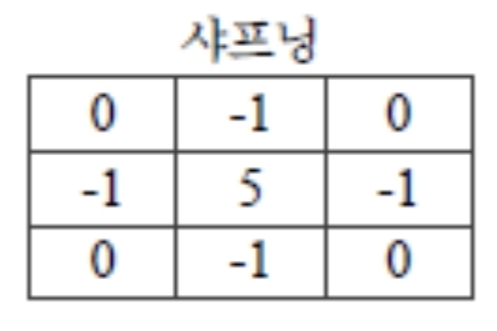
- 특징: 자기 자신의 명암 강조 - 주변의 평균값
- “지역 평균과의 차를 강조”하는 샤프닝 필터 예시.
- 에지 검출(1차 미분형)
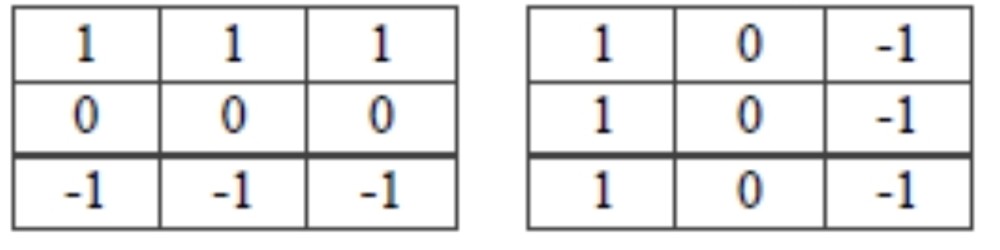
- Sobel: 수직/수평 마스크로 경계 강조.
- 미분은 노이즈에 민감 → 스무딩 후 미분이 정석
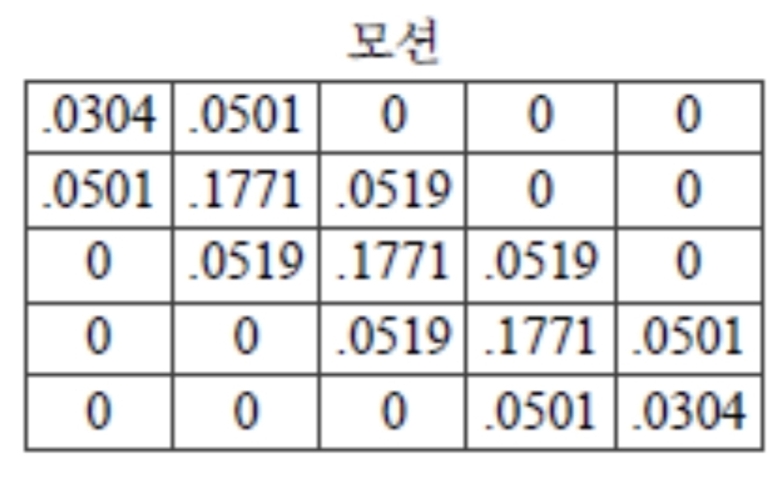
- 모션 필터
- 비선형 필터
- Median: 임펄스(솔트 페퍼) 노이즈에 강함.

- 최소, 최대 제외 후 중앙값 사용
2.5. 패딩
2.5.1. Zero padding (제로 패딩, constant=0)
- 정의: 영상 밖을 모두 0으로 채워넣고 필터링.
- 1D 예시:
[...] a b c [...] → 제로 패딩 후: [0 a b c 0]
- 수식(2D): 바깥 좌표
(x,y)가 범위 밖이면 I_padded(x,y)=0.
- 장단점: 계산이 단순하고 속도가 빠르지만, 가장자리에서 어둡게 끌리는(검게 번짐) 인공물이 생기기 쉽다.
2.5.2. Replicate padding (복제, 클램핑, edge)
- 정의: 영상 밖의 값을 가장자리 픽셀값으로 복제하여 연장.
- 1D 예시: 원본
a b c → 패딩 후 [a a b c c] (왼쪽 바깥은 a로, 오른쪽 바깥은 c로 채움)
- 수식(2D): 범위 밖 좌표를 가장 가까운 유효 좌표로 클램프: $I_padded(x,y)=I(clamp(x,0,W-1), clamp(y,0,H-1)$
- 장단점: 경계에서 값의 급격한 하락(0으로 가는) 현상을 막아 엣지 보존이 제로 패딩보다 낫다. 다만 긴 평탄대(plateau) 가 생겨 살짝 뭉개질 수 있다.
2.5.3. Reflect padding (미러, 반사)
- 정의: 영상 바깥을 거울 반사처럼 대칭 확장.
- 1D 예시(반복 없음, OpenCV의
BORDER_REFLECT_101/NumPy의 reflect):
- 원본
a b c → 패딩 후 [b a b c b] (가장자리 값은 한 번만 사용하고 그 바깥은 거울처럼 반사)
- 대안 변형(대칭 포함, 일부 라이브러리
symmetric):
a b c → [a b a b c c]처럼 가장자리 값을 다시 한 번 포함하는 미러.
- 장단점: 경계에서 연속적인 그라디언트를 유지해 블러/가우시안 필터 등에서 경계 인공물 최소화. 대개 시각적으로 가장 자연스럽다.
2.5.4. 패딩 사용 예시
- 블러/가우시안/저주파 필터:
reflect 권장(경계 자연스러움).
- 엣지 검출(소벨/라플라시안):
reflect 또는 replicate (제로 패딩은 경계에서 가짜 엣지 유발 가능).
- 딥러닝 전처리에서 일관성/단순성: 구현·성능 고려해
replicate가 흔함(프레임워크 기본도 자주 이 모드).
- 수치 안정성/특정 이론 가정(예: 경계=0):
zero 선택.









Comments