선분 검출

1. 에지 연결과 표현

성분	주변 에지 성분 개수
끝점	1
통과점	2
분기점	3개 이상

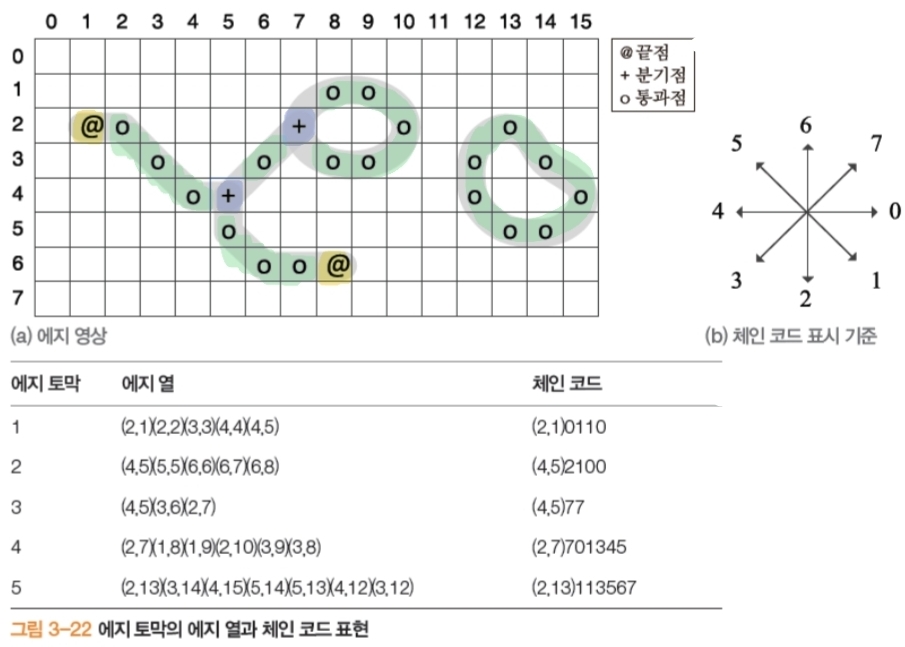
에지 성분만 표현하는 방법
- 체인 코드: 에지(또는 이진 경계)를 순회하며 방향만 기록해 경계를 표현하는 방식이다
- 에지 토막: 연결된 에지 픽셀을 짧은 곡선/선분 단위의 폴리라인으로 묶어 표현한다

poly line: 여러 개의 선 부분이 연속적으로 연결된 곡선 또는 직선 형태의 경로

2. 선분 근사

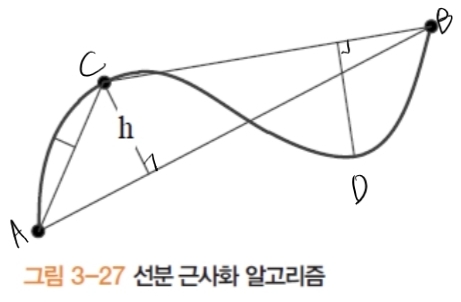
두 끝점을 잇는 직선으로부터 가장 먼 점까지의 거리 $h$가 임계값 이내가 될 때까지 선분 분할을 재귀적으로 반복한다

3. Voting Schemes

Alt Images 투표(voting) 기반 모델 추정: 특징(feature)들이 자신과 양립 가능한 모델들에 표를 던지고, 표가 많이 모인 모델을 정답으로 뽑는다 e.g. 허프 변환(Hough transform), RANSAC의 합의 집합(consensus set)

3.1. 개념

각 특징 $f_i$가 “나와 부합(compatible) 하는” 모든 모델 파라미터 $\theta$에 표를 던짐 → 누적기(accumulator)에 카운트
잡음(outlier)은 표를 여기저기 흩뿌려서 어느 한 모델에도 표가 집중되지 않음
일부 특징이 누락(occlusion, missing data) 되어도, 남은 특징들이 같은 좋은 모델에 표를 몰아주면 검출 가능

3.2. 노이즈

3.2.1. 노이즈가 미치는 영향

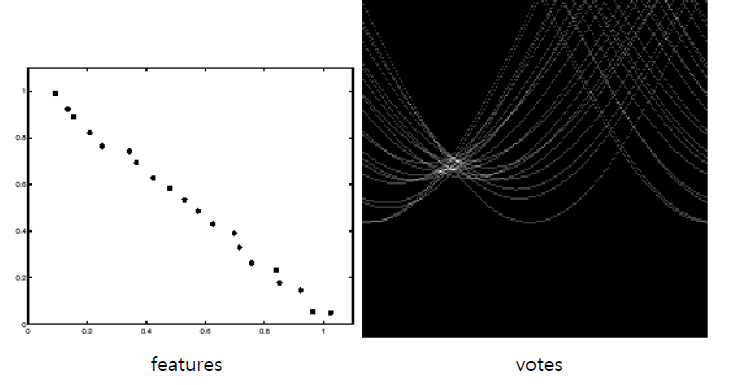
피처 공간의 균일 잡음은 누적 배열에 허위(spurious) 피크를 만든다. 노이즈가 커질수록 최대 득표 수 자체도 증가해 진짜 피크가 흐려지고(peak fuzziness) 위치도 불안정해진다.

3.2.2. 노이즈 대응 전략 (Hough 기준)

격자(grid)/이산화(discretization) 해상도 선택
- 너무 조잡(coarse): 서로 다른 선/모델이 한 버킷에 섞여 득표 과다.
- 너무 세밀(fine): 같은 모델 점들도 미세 오차로 서로 다른 버킷에 흩어짐.
누적 배열 평활화: 이웃 bin까지 증가(smoothing)해 노이즈로 인한 들쭉날쭉함을 완화.
무관한 피처 제거: 큰 그래디언트를 가진 에지 포인트만 사용해 투표 품질을 올림.

3.2.3. 장단점

장점: 부분 가림/비국소성에 강함, 복수 객체 동시 검출, 노이즈에 어느 정도 강인(노이즈 점들은 한 bin에 일관되게 모이기 어려움).
단점: 파라미터 수가 늘면 탐색 복잡도 급증, 비목표 형태가 허위 피크 생성, 격자 크기 선택이 어렵다

3.3. 동작

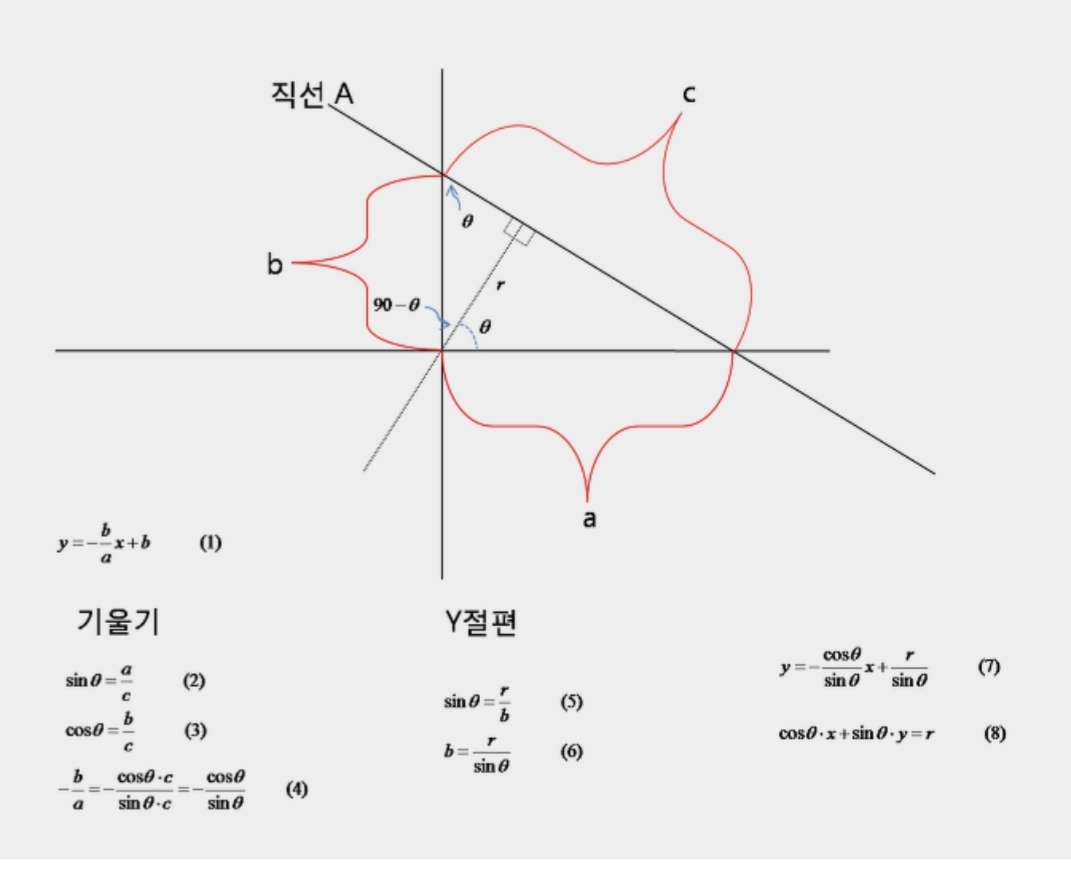
모델 정의: 예) 직선 $\rho = x\cos\theta + y\sin\theta$ (극좌표)
파라미터 공간 분할: $(\rho,\theta)$ 격자 만들기
투표: 에지 픽셀 등 특징점 $(x,y)$마다 가능한 $\theta$를 훑으며 해당 $\rho$ 계산 → 해당 버킷 $(\rho,\theta)$에 +1
피크 찾기: 누적기가 큰 버킷(피크)을 모델 후보로 선택
정제(refine): 피크에 투표한 점들을 모아 최소자승 등으로 파라미터 미세 조정

3.4. 특징

3.4.1. 장점

잡음/가림(occlusion)·부분적 누락에 매우 강건
- 잡음 특징: 호환 가능한 모델이 제각각 → 표가 분산 → 큰 피크를 못 만듦
- 누락 데이터: 일부 표가 빠져도 남은 표가 임계치 이상 모이면 피크 유지 → 검출 가능
복수 개의 모델(여러 직선/원)도 피크 여러 개로 동시에 검출
병렬화 쉬움

3.4.2. 단점

파라미터 차원이 커질수록 격자 수 폭증(계산·메모리 부담, 양자화 오차)
버킷 크기/임계치에 민감(과도한 스무딩은 피크 손실, 너무 세분화하면 잡음 피크 증가)
근접한 피크 병합/해석이 필요

4. 허프 변환(Hough Transform)

4.1. 개념

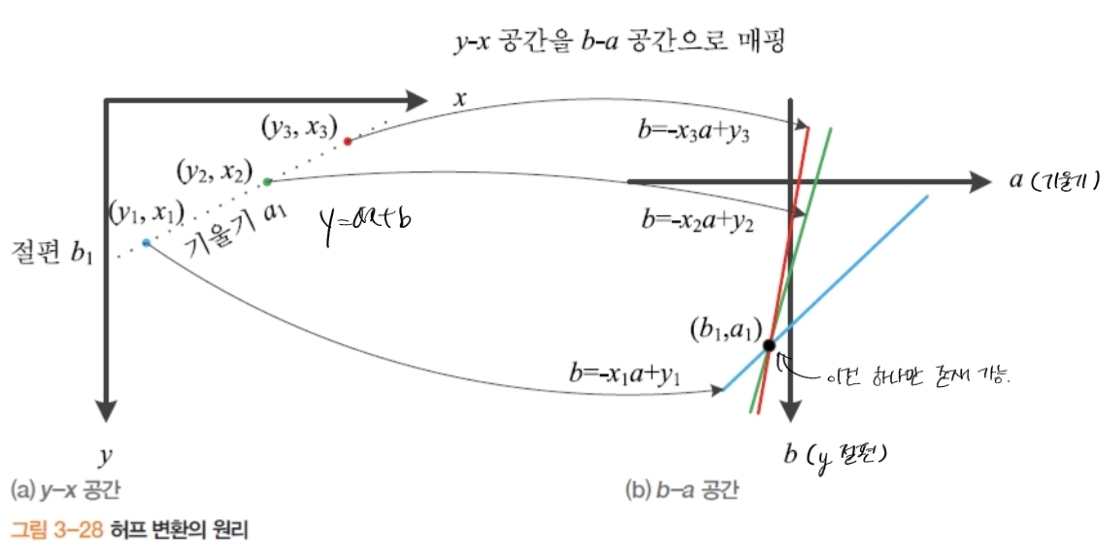
허프 변환: 차원의 변환, 좌표계의 변환
- 에지 연결 과정 없이 선분 검출 (전역 연산을 이용한 지각 군집화)
- 영상 공간 y-x 를 기울기 절편 공간 b-a 로 매핑
- 일반 절차:
  1. 파라미터 공간을 격자(bin) 로 이산화
  2. 영상의 각 에지점이 가능한 모든 파라미터 bin에 투표
  3. 누적배열의 피크를 검출.
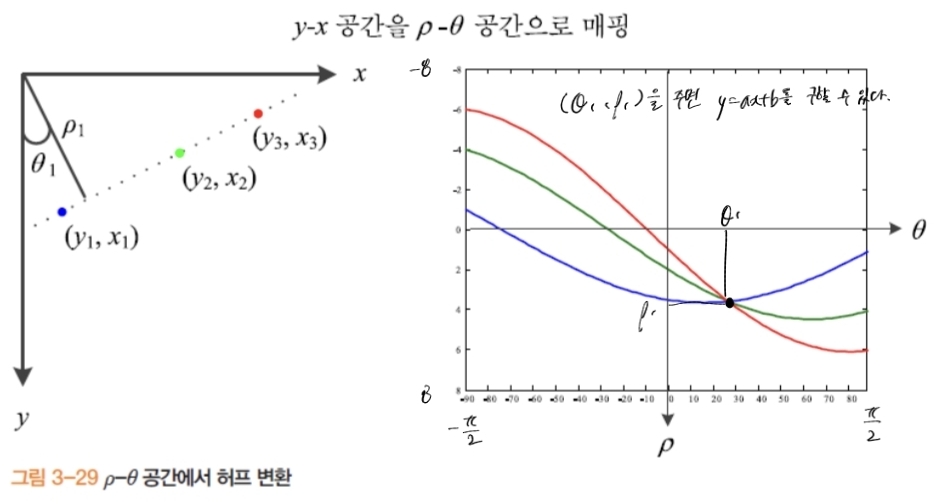
파라미터 범위가 무한, 수직선에서 $m\to\infty$ 문제가 발생.
- 극좌표 대안: $\rho=x\cos\theta+y\sin\theta$

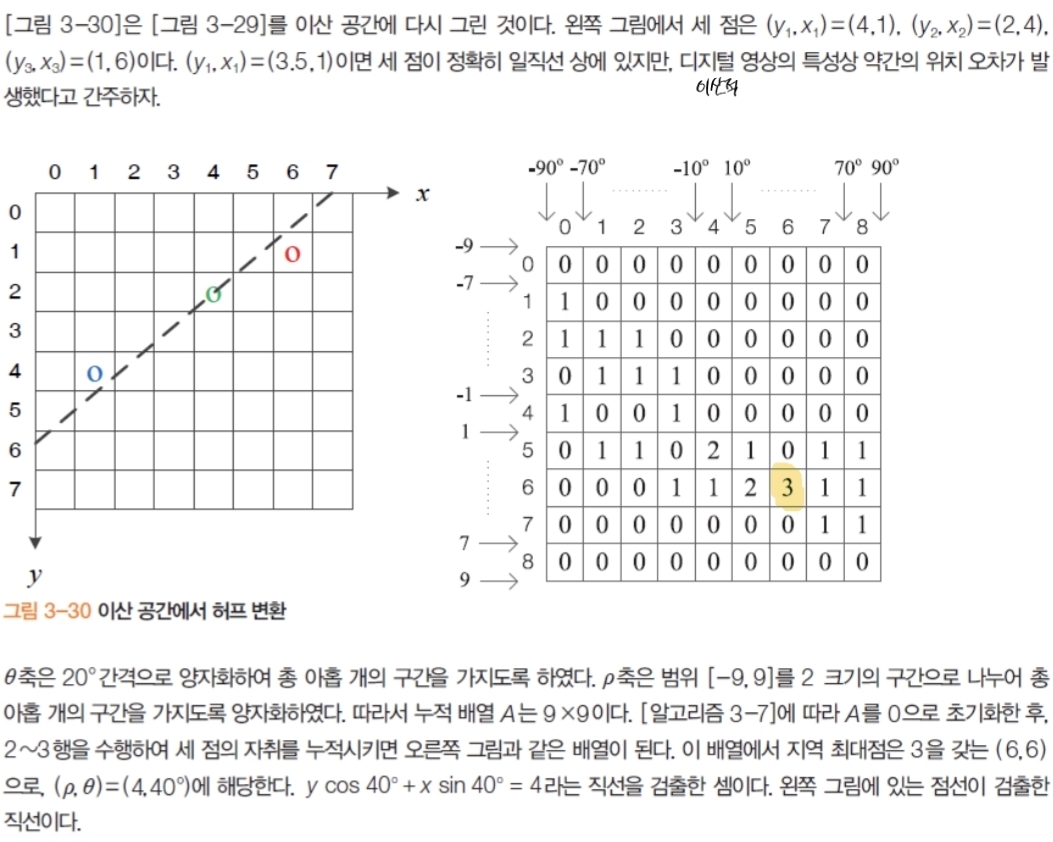
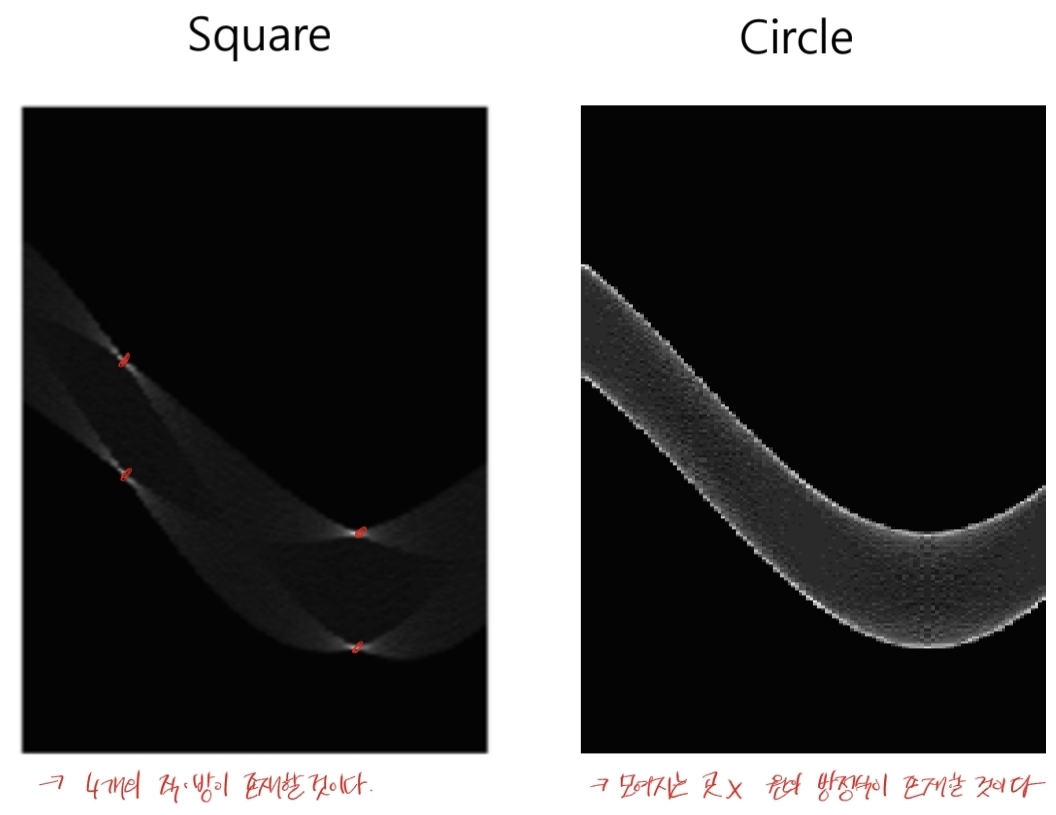
4.2. 원 검출

원 검출: 3차원 누적 배열 사용
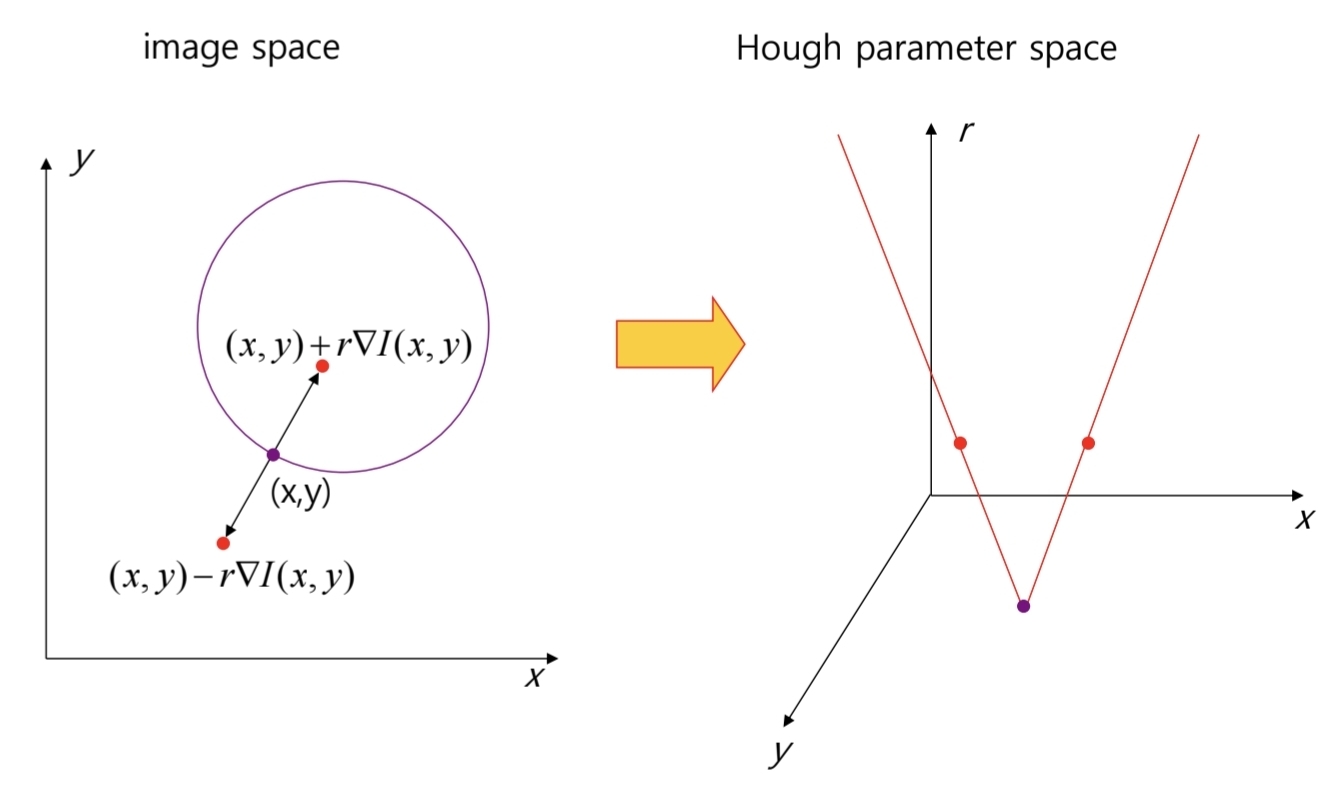
- $(y - b)^2 + (x-a)^2 = r^2$
해석 관점: 영상의 한 점 $(x_0,y_0)$은 허프 공간에서 사인곡선이며, 두 점 곡선의 교차가 두 점을 지나는 직선의 파라미터.

4.3. 특징

장점:
- 가림(occlusion)·비지역성에 강함
- 다중 인스턴스 검출
- 어느 정도 노이즈 강건.
단점:
- 파라미터 수↑ 시 시간/메모리 지수적 증가
- 비목표 형상이 허위 피크 유발
- 격자 크기 선택 난이도

~~8 * 8 사이즈에서 9 * 9 사이즈가 된 걸 보면 허프 변환이 모든 상황에서 더 효율적인 것은 아닌 것 같다~~

5. Implicit Shape Model (ISM)

훈련: 관심점 주변 패치 → 클러스터링으로 코드북 구성 → 각 코드북 항목에 대해 객체 중심 상대 위치(변위)들 저장.
테스트: 패치→가까운 코드북 항목으로 매칭 → 객체 중심 후보에 투표 → 투표공간 최대값 탐색 → 저장된 마스크들을 가중 결합해 분할.
세부 이슈: 투표공간이 연속이므로 클러스터링 필요, 스케일은 다중 스케일 탐색 또는 특징 자체의 특징 스케일 활용, 마지막에 검증 단계(정교 템플릿·마스크 전이) 중요.

5. RANSAC — 불량치(outlier) 견고 추정

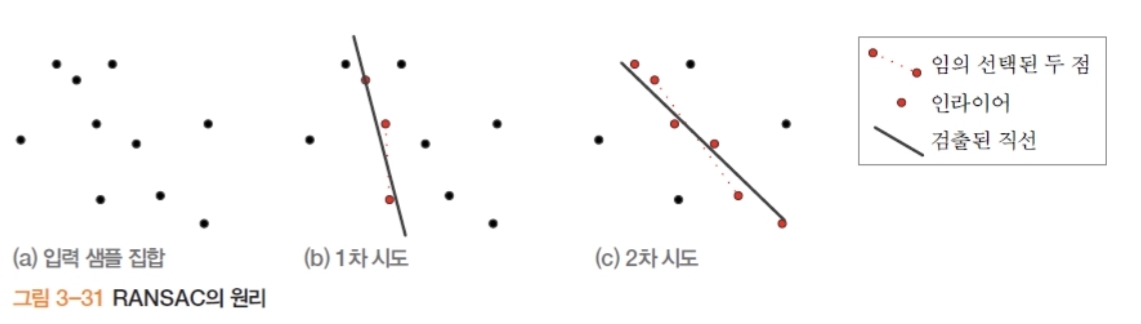
정의/배경: Fischler & Bolles(1981). 인라이어 집합을 찾아 모델을 견고하게 적합(무작위 표본 기반). 선분 검출에선 모델을 $y=ax+b$로 둔다.
동작
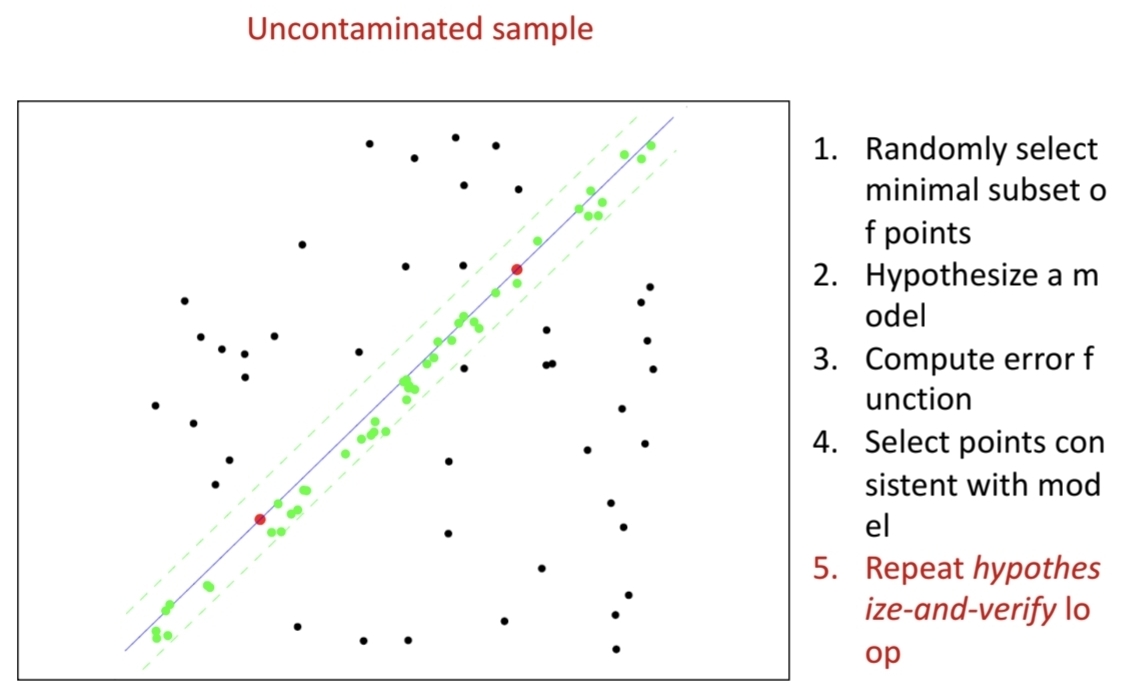
- 1. 최소 표본 무작위 선택, 무작위로 두 점을 골라 직선의 방정식을 구함
  2. 모델 가설, 구한 방정식으로부터 일정 범위의 속한 점들이 전체의 몇 %인지 구함
  3. 오차함수 계산
  4. 일치(inlier) 집합 선택, 전체 80%가 포함되지 않으면 두 점을 버림
  5. 반복.
확장 포인트: 점-점 매칭쌍 $X={(a_i,b_i)}$ 입력도 처리하도록 일반화(기하 추정에 활용).
알고리즘

5.1. Hough V.S. RANSAC

허프: 파라미터가 저차원이고 폐형식(직선·원 등)이 있을 때 단순·효율적.
RANSAC: 복잡하거나 고차원 모델, 불균일한 불확실성에서 유리. 표본 추출 → 가설 모델 → 인라이어 카운트로 투표와 유사한 합의를 구함.

COMPUTER_VISION

[COMPUTER VISION] Voting Schemes

목차