목차
히스토그램
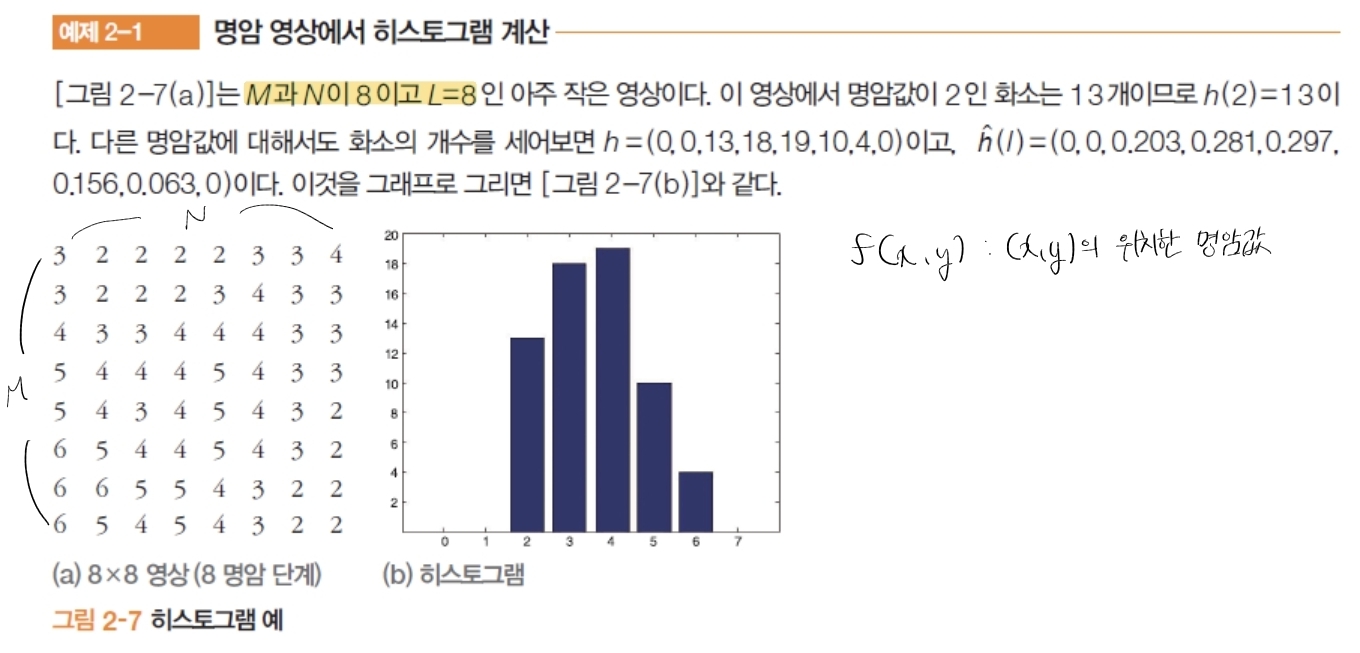
1. 히스토그램
- 정의: $[0, \, L-1]$ 사이의 명암값이 각각 영상 등장 빈도 계산, 밝기(또는 색상) 값의 분포를 세는 함수
- 히스토그램: \(h(k)=\{(i,j)∣f(i,j)=k\}\)
- 정규화 히스토그램: \(0 \leq p(k)=\frac{h(k)}{MN} \leq 1\)
- 누적 히스토그램: \(c(k)=\sum_{t=0}^{k}p(t)\)
- 알고리즘:
- 예제
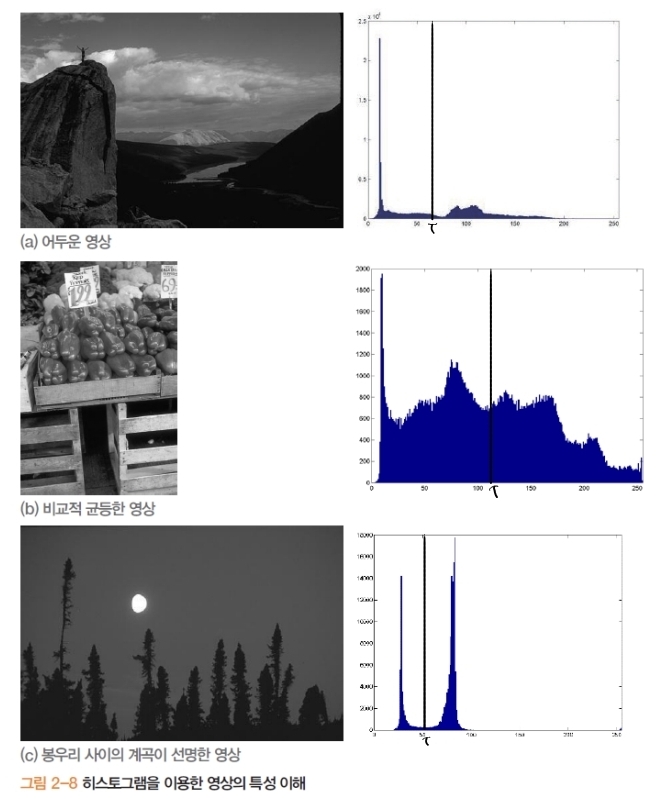
- 용도: 영상 특성 파악(밝기/대비/노출), 이진화 임계값 선정의 사전 지표.
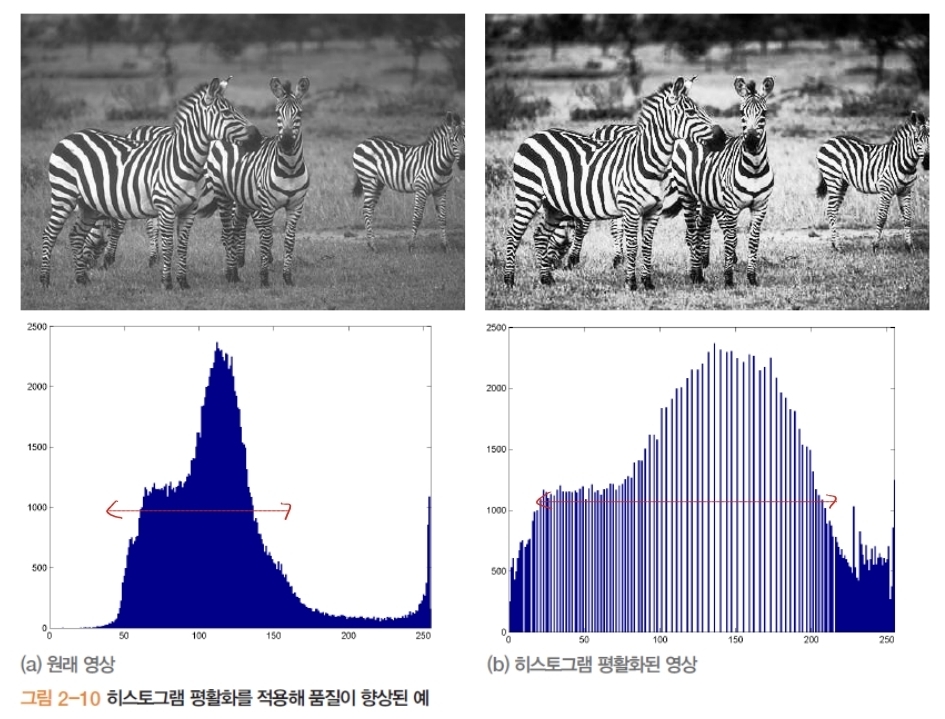
2. 히스토그램 평활화 (Histogram Equalization)
- 히스토그램을 평평하게 만들어 주는 연산
- 명암의 동적 범위 확장 → 영상 품질 향상
- 누적 히스토그램 ($c(\cdot)$) 을 매핑 함수로 사용
- “뭉쳐있다” → 특정 구간
[a, b]가 뭉쳐져있으면 CDF의[a, b]구간에서 가파르게 증가한다 -
\[l_{out} = T(l_{in}) = \text {round} (c(l_{in}) \times (L-1))\]
- $round$: 정수형 변환
- $c(l_{in})$: 누적합
- $L-1$: 0 ~ 255
-
\[c(l_{in}) = \sum ^ {l_{in}} _ {l = 0} \hat h (l)\]
- $l = 0$: 가중치
- 예제

- 0~1 → 0, 2 → 1, 3 → 3, 4 → 5, 5~7 → 7로 매핑되는 것을 볼 수 있다.
- Histogram Stretching V.S. Histogram Equalization
- Histogram Stretching: min ~ max 값을 0 ~ 255로 선형적으로 늘려줌 → min 값이 0, max 값이 255 면 의미가 없음
- Histogram Equalization: 분포가 몰린 부분을 비선형적으로 늘려줌
- 적용 여부 판단 조건
- 영상의 밝기 분포
- 영상 처리 목적: 시각적 개선(대비 향상 목적), 후처리 전처리 단계(명암 대비 균질화), 원본 톤 유지 필요 여부
- 영상 종류 및 채널 특성: 단일 채널 영상, 컬러 영상(밝기 성분만), 영상 크기와 양자화 수준
- 잠재적 부작용: 노이즈 증폭, 밴딩 현상, 원본 분위기 상실
“히스토그램과 누적 히스토그램을 만든 뒤, 픽셀값을 매핑해 밝기 분포를 재조정한다”
3. 히스토그램 역투영 & 얼굴 검출
- 아이디어: 학습(또는 모델) 영상의 히스토그램을 매핑 함수로 사용하여, 입력 영상의 각 화소를 신뢰도 맵으로 변환. 보통 2개의 차원 분포를 확인함.
- 절차: 대상 모델의 (정규화) 히스토그램 ($h_r$) 계산 → 입력 화소값을 ($h_r$)로 사상하여 back-projection 맵 생성 → 평활화/후처리 → 최대값/영역 추출.
- 2차원 히스토그램 계산 알고리즘
- 예시: 2D 히스토그램(예: 피부색) 기반 얼굴 검출.
- \[h_r(i, j) = min(\frac{\hat h_m(i, j)}{\hat h_j(i, j)}, 1), \; 0 \leq i, \; j \leq q-1\]
- $h_r(i, j)$: 모델과 입력 영상의 유사도
- $\hat h_m(i, j)$: 모델에 대한 정규화 히스토그램
- $\hat h_j(i, j)$: 입력 영상에 대한 정규화 히스토그램
- 특성:
- 장점: 배경 제어가 가능한 상황에서 유리, 이동/회전 불변, 가림에도 비교적 강건.
- 한계: 유사 분포물 혼동(비슷한 색 분포를 갖는 다른 물체 구별 못함), 대상 색 분포가 여러 개인 경우 오류 증가.
- 히스토그램 역투영 알고리즘
“경계/질감이 약한 영역도 분포 기반으로 찾아낼 수 있다”
4. 이진 영상: 임계값 & 오츠(Otsu) 알고리즘
- 이진화:
- 그레이스케일 → 흑/백으로 변환.
- \[b(j,i) = \begin{cases} 1, & f(j,i) \ge T,\\[4pt] 0, & f(j,i) < T \end{cases}\]
- 임계값 방법
- 두 봉우리 사이의 계곡에 임계값 T로 결정
- 자연영상은 계곡 탐지가 어려움
4.1. Otsu 알고리즘
- 흑 그룹과 백 그룹 각각이 균일할수록 좋다
- 균일성은 분산으로 측정 → 클래스 내 분산 최소(= 클래스 간 균일성 최대)
- 분산의 가중치 합 $v_{within}(t)$을 목적 함수로 이용한 최적화 알고리즘
- 조명 균일·배경/전경 분리가 비교적 명확할 때 강력.
- 수식
- \[T' = \arg\min_{t \in \{0,1,\dots,L-1\}} v_{\text{within}}(t)\]
- \[v_{\text{within}}(t) = w_0(t) v_0(t) + w_1(t) v_1(t)\]
- \[w_0(t) = \sum_{i=0}^{t} \hat{h}(i), \qquad w_1(t) = \sum_{i=t+1}^{L-1} \hat{h}(i)\]
- \[\mu_0(t) = \frac{1}{w_0(t)} \sum_{i=0}^{t} i \hat{h}(i), \qquad \mu_1(t) = \frac{1}{w_1(t)} \sum_{i=t+1}^{L-1} i \hat{h}(i)\]
- \[v_0(t) = \frac{1}{w_0(t)} \sum_{i=0}^{t} \hat{h}(i)\big(i - \mu_0(t)\big)^2, \qquad v_1(t) = \frac{1}{w_1(t)} \sum_{i=t+1}^{L-1} \hat{h}(i)\big(i - \mu_1(t)\big)^2\]
- 최적화 수식
- \[T' = \arg\max_{t \in \{0,1,\dots,L-1\}} v_{\text{between}}(t)\]
- \[v_{\text{between}}(t) = w_0(t)\big(1 - w_0(t)\big)\big(\mu_0(t) - \mu_1(t)\big)^2\]
- 초깃값: \((t=0):\quad w_0(0) = \hat{h}(0),\quad \mu_0(0) = 0\)
- 순환식 (t>0): \(\begin{align} & w_0(t) = w_0(t-1) + \hat{h}(t) \\ & \mu_0(t) = \frac{w_0(t-1)\mu_0(t-1) + t\,\hat{h}(t)}{w_0(t)} \\ & \mu_1(t) = \frac{\mu - w_0(t)\mu_0(t)}{1 - w_0(t)} \end{align}\)
- 알고리즘
실전 팁: 조명 변화가 크면 적응 임계값(블록별 T) 나 선행 평활화를 병행.
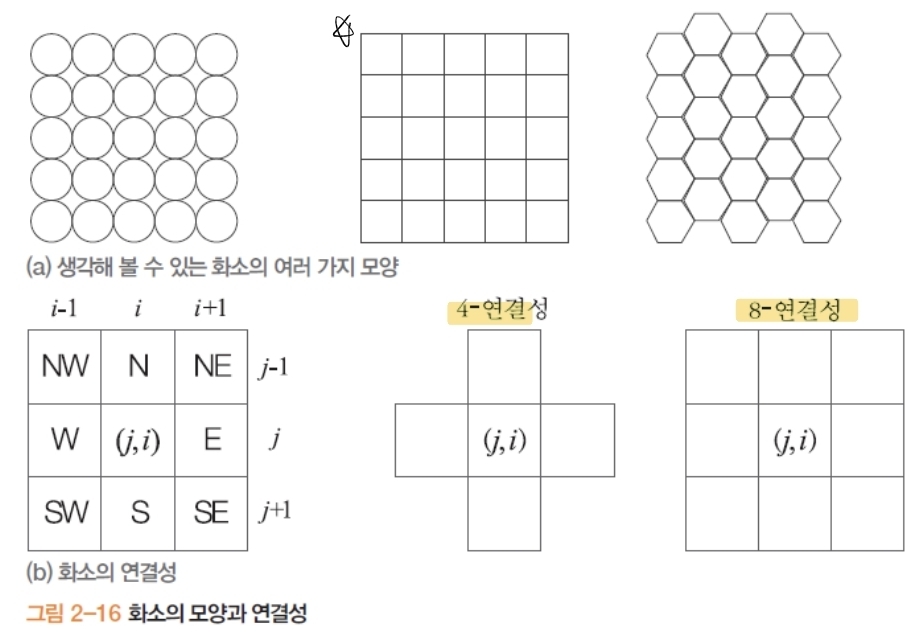
5. 연결 요소(Connected Components) 라벨링
- 연결성 정의: 4-연결/8-연결로 화소 이웃을 규정, 동일 라벨로 군집화.
- 구현 관점:
- Flood-fill(범람 채움): 직관적이나 재귀 사용 시 스택 오버플로 주의.
- Flood-fill(범람 채움): 직관적이나 재귀 사용 시 스택 오버플로 주의.








Comments