[AI] Gradient Clipping

11 Nov 2025 • AI

목차

  1. 정의
  2. 배경
    1. 신경망의 gradient(기울기)
    2. Gradient Vanishing/Exploding
  3. 수식
  4. 종류
  5. 장단점
    1. 장점
    2. 단점
  6. 참고

Gradient Clipping

1. 정의

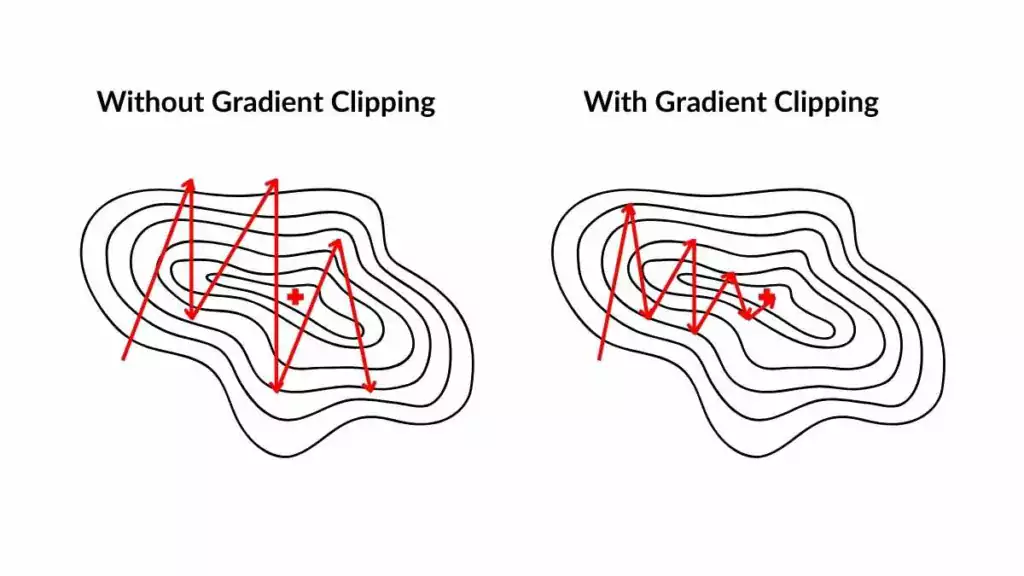
Alt Images

Gradient Clipping: 기울기(gradient)의 크기가 너무 커지는 것(기울기 폭발) 을 방지하기 위해 기울기의 크기(norm) 를 일정 한도 이하로 잘라내는(clipping) 기법이다.

2. 배경

2.1. 신경망의 gradient(기울기)

신경망의 학습 과정에서는 역전파(Backpropagation)를 통해 각 파라미터의 기울기(gradient)가 계산된다. 기울기

  • 파라미터에 대한 함수의 변화율을 나타내는 미분값.
  • 딥러닝에서 네트워크 내 각 파라미터에 대한 손실 함수의 변화.

2.2. Gradient Vanishing/Exploding

  • Gradient Vanishing: gradient가 역전파 과정에서 매우 작아져 효과적으로 학습하지 못해 학습 속도가 낮아지는 문제
  • Gradient Exploding: gradient가 역전파 과정에서 매우 커져 파라미터 업데이트가 불안정해지고 수렴이 지연되는 문제 → 손실이 발산, 학습 불안정, NaN 발생

3. 수식

\(\frac{\partial \varepsilon}{\partial \boldsymbol{\theta}} \leftarrow \begin{cases} \displaystyle \frac{\text{threshold}}{\lVert \hat{\boldsymbol{g}} \rVert}\,\hat{\boldsymbol{g}} & \text{if }\lVert \hat{\boldsymbol{g}} \rVert \ge \text{threshold}\\[6pt] \hat{\boldsymbol{g}} & \text{otherwise} \end{cases} \quad\text{where}\quad \hat{\boldsymbol{g}} = \frac{\partial \varepsilon}{\partial \boldsymbol{\theta}}\)

  • $ε$: 손실(loss)
  • $θ$: 모델 파라미터 벡터
  • $\hat{\boldsymbol{g}}=\dfrac{\partial \varepsilon}{\partial \boldsymbol{\theta}}$​: 원래(미가공) 기울기
  • $∥⋅∥$: 보통 L2 norm(길이/크기). 문맥에 따라 L1/Lp도 가능

  • threshold ($\tau$라고도 표기): 허용하는 최대 기울기 크기(하이퍼파라미터)

  • $∥g^​∥≥threshold$이면 scale factor $\frac{\text{threshold}}{\lVert \hat{\boldsymbol{g}} \rVert} \le 1$로 일괄 축소 → 방향은 같고 크기만 threshold.
  • 작으면 그대로 사용.

4. 종류

  • Norm Clipping: 전체 gradient 벡터의 norm이 threshold를 넘으면 값 조정
  • Value Clipping: gradient의 각 원소별로 절대값을 제한
  • Adaptive Clipping: 파라미터별로 다른 한도를 적용

5. 장단점

5.1. 장점

  • Gradient Exploding 방지
    • 안정화 학습: gradient 값에 최대 크기를 제한함으로써 불규칙한 매개변수 업데이트 발생을 방지한다.
    • 안정성 보장: gradient 크기에 대한 제한은 최적화 프로세스의 안정성을 유지해 극단적인 업데이트로 인한 발산을 방지한다.
  • Gradient Vanishing 방지
    • 심층 레이어에서 학습 촉진: gradient가 지나치게 작아지는 것을 제한함으로써 유용한 정보를 심층 신경망 레이어로 전파하는 데 도움이 된다.
    • 효과적인 학습 촉진: gradient vanishing을 방지하면 전체 네트워크에서 더 효과적인 학습이 가능해져 전반적인 모델 성능이 향상된다.
  • 모델 안정성 및 수렴성 향상
    • 일관된 훈련: 제어된 gradient는 매개변수 값이 보다 일관된 업데이트로 이어지고, 학습 중에 원활한 수렴을 촉진한다.
    • 효율적인 최적화: gradient 크기를 관리함으로써 더욱 효율적인 최적화에 기여해 신경망이 더욱 안정적이고 빠르게 수렴할 수 있게 한다.

5.2. 단점

  • 임계값 감도
    • 모델 성능에 미치는 영향: 임계값을 너무 낮게 설정하면 수렴에 방해가 되고, 너무 높게 설정하면 학습이 안정화되지 못할 수 있다.
  • 학습 역학의 붕괴
    • 정보 손실: 공격적인 clipping으로 인해 중요한 gradient 정보가 삭제되어 모델의 학습 능력에 영향을 미칠 수 있다.
    • 감소된 모델 표현력: 지나치게 공격적인 clipping은 복잡한 패턴을 포착하는 모델의 능력을 제한할 수 있다.
  • 복잡성 및 유지 관리
    • 프레임워크 종속성: 구현은 다양한 딥 러닝 프레임워크에 따라 다를 수 있으므로 일관된 사용을 위해서는 조정이 필요하다.
    • 추가 하이퍼파라미터: 임계값과 방법을 관리하면 신중한 조정이 필요해지므로 추가 하이퍼파라미터가 발생한다.
  • 상황에 따른 효과성
    • 아키텍처 민감도: 네트워크 아키텍처와 작업 복잡성에 따라 효과가 달라질 수 있다.
    • 영향 제한: gradient가 원래 안정적인 시나리오에서는 효과가 그다지 크지 않을 수 있다.
  • 과적합
    • 일반화에 미치는 영향: 지나치게 공격적인 clipping은 학습 세트에서는 좋은 성능을 보이는 모델이 생성되지만, 보이지 않는 데이터에서는 성능이 떨어져 과적합이 발생할 수 있다.

참고

 AI  DEEP_LEARNING

Comments

Newest Posts