목차
에지(Edge)
- 유용성: 물체 경계를 안정적으로 표시, 매칭·정합·분할의 핵심 단서.
- 어려움: 잡음 증폭, 약한/누락(edge miss)·거짓 에지(false edge), 조명/질감 변화, 스케일 의존성.
1. 에지 검출 기초
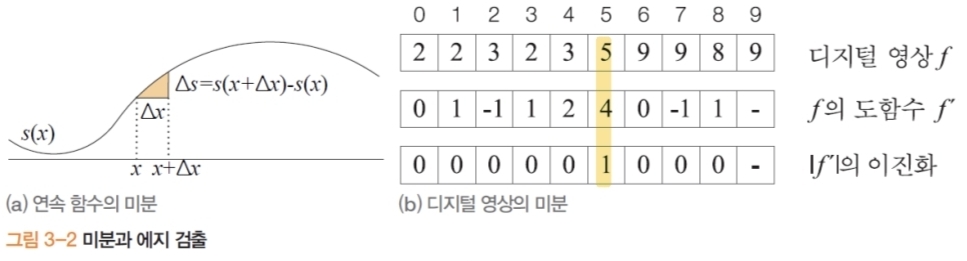
1.1. 연속/이산 미분
- 연속 공간 미분: \(\displaystyle f'(x)=\frac{ds}{dx} = \lim_{\Delta x\to 0} \frac {s(x + \Delta x) - s(x))}{\Delta x}\) 는 밝기 변화율 → 에지에서 극값(피크).
- 이산 공간 미분: \(f'(x) = \frac{df}{dx} = \lim_{\Delta x\to 0} \frac {f(x + \Delta x) - f(x))}{\Delta x} = f(x{+}1)-f(x)\)
- → 에지 연산자 마스크: $\begin{bmatrix} -1 & 1\end{bmatrix}$
-
- 2차 미분: \(\begin{align}
f''(x) &= \frac{d^2f}{dx^2}= f'(x) - f'(x-1) \\
&= (f(x+1)-f(x)) - (f(x)-f(x-1)) \\
&=f(x+1)+f(x-1)-2f(x)
\end{align}\)
- 마스크: $\begin{bmatrix} 1 & -2 & 1\end{bmatrix}$
- 에지 검출 과정
- 1차 미분에서 봉우리, 2차 미분에서 영교차를 찾음
1.2 에지 모델과 1차/2차 미분
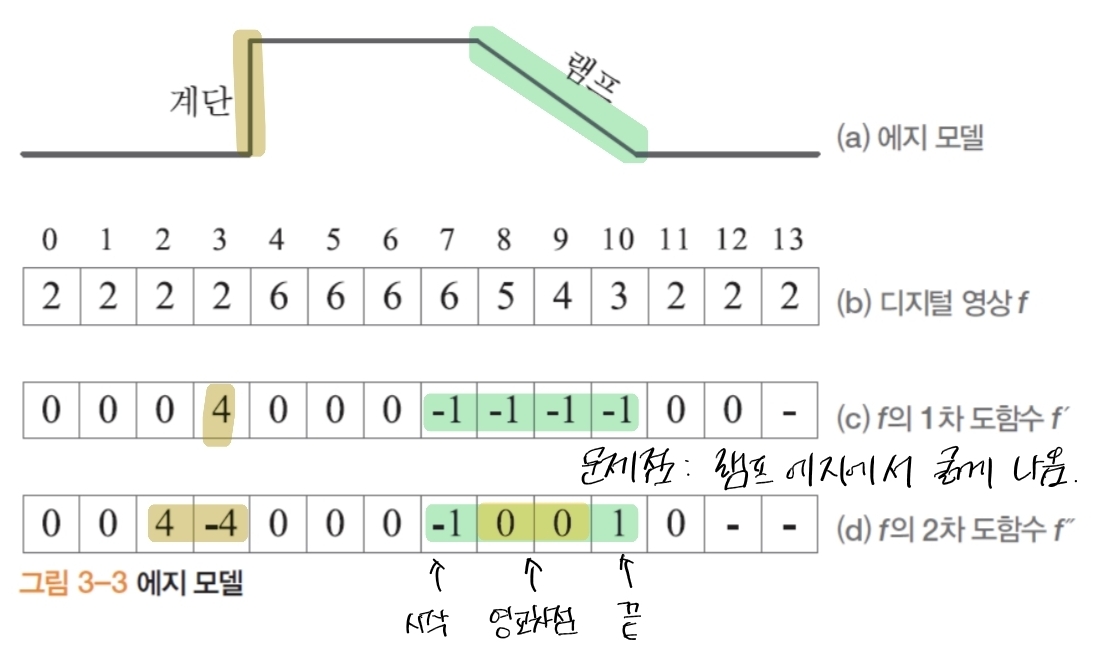
- 계단(step) 에지: 밝기 불연속. 1차 미분=피크(±), 2차 미분=0-교차(zero-crossing).
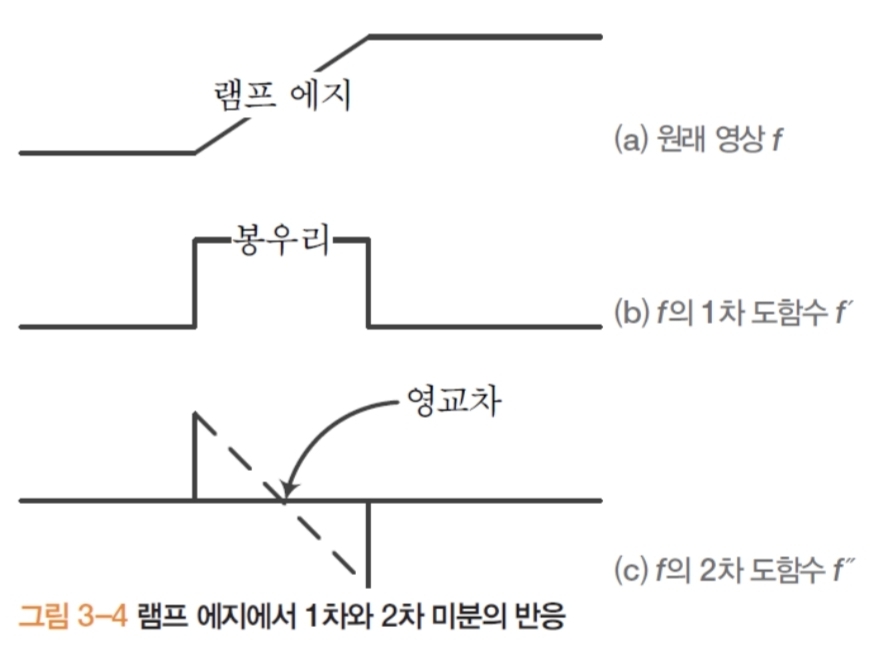
- 램프(ramp) 에지: 실제 영상은 주로 램프(기울기 완만). 잡음 때문에 스무딩 선행 필요.
- 선(line) 에지: 밝기 얇은 봉우리/골. 2차 미분 응답 유용.
1.3 잡음과 스무딩: 가우시안/가우시안 미분
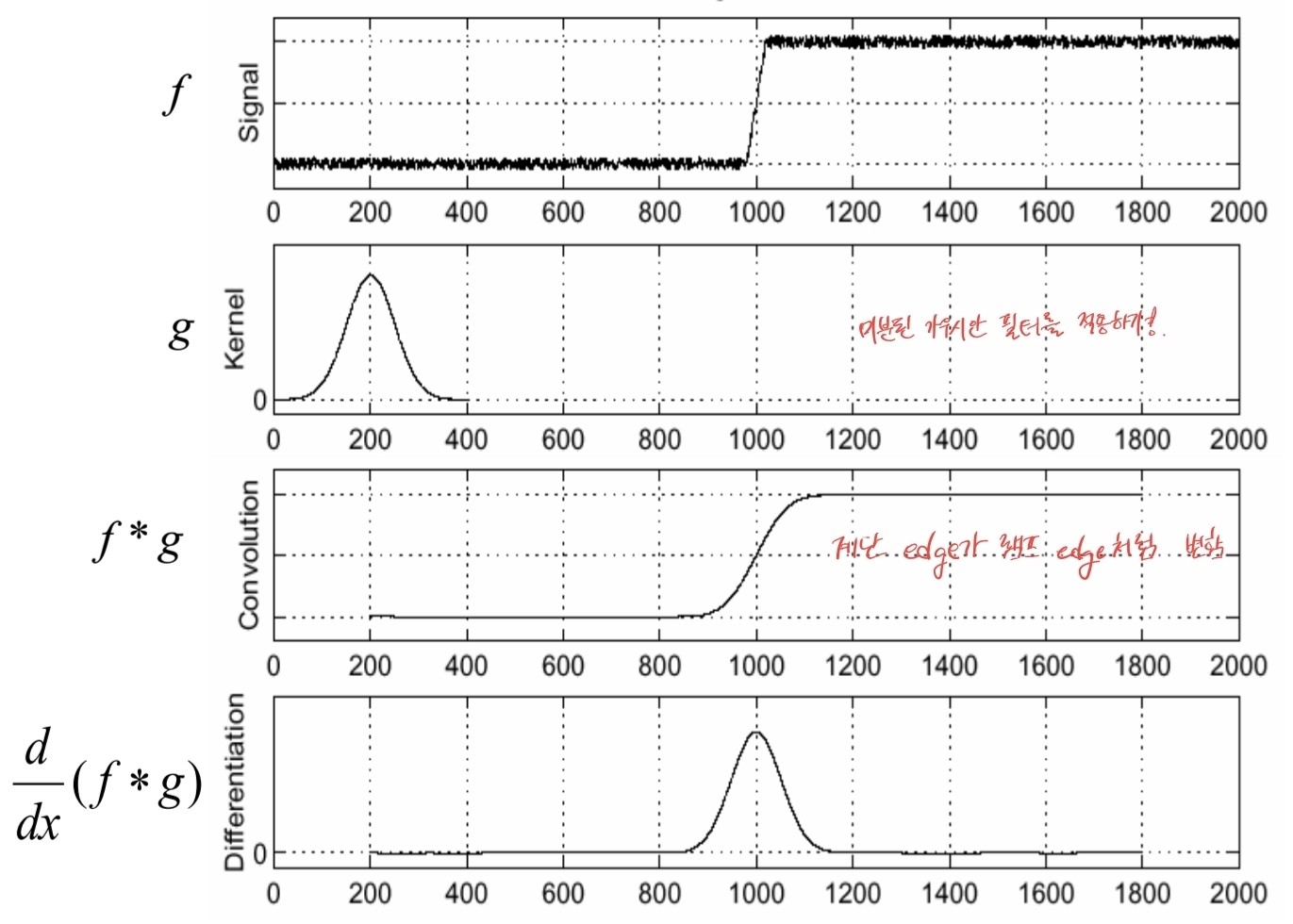
- 미분은 고주파(잡음) 증폭 → 가우시안 스무딩 $G_\sigma$ 선행:
- $I_\sigma = G_\sigma * I,\quad \partial_x I_\sigma = (\partial_x G_\sigma) * I$
- 가우시안은 분리 가능 → $O(k^2)$ → $O(2k)$로 연산량 감소.
- 커널 크기: $\text{size} \approx 6\sigma+1$ (가장 작은 홀수) 권장.
1.4. 에지 모델과 연산자
- $\Delta x = 1$이 잡음에 너무 민감 → $\Delta x = 2$로 확장
- \[f'(x) = \frac{df}{dx} = \frac{f(x+1)-f(x-1)}{2}\]
- 마스크: $\begin{bmatrix} -1 & 0 & 1\end{bmatrix}$
- 2차원으로 확장
- \[\begin{align} \nabla f(y,x) &= (\frac{\partial f}{\partial y}, \frac{\partial f}{\partial x}) = (d_y , d_x) \\ &= (f(y{+}1,x)-f(y{-}1,x)), (f(y,x{+}1)-f(y,x-1)) \end{align}\]
- 마스크: \(m_y=\begin{bmatrix}-1\\0\\1\end{bmatrix},\qquad m_x=\begin{bmatrix}-1&0&1\end{bmatrix}\)
- 기본 미분 커널
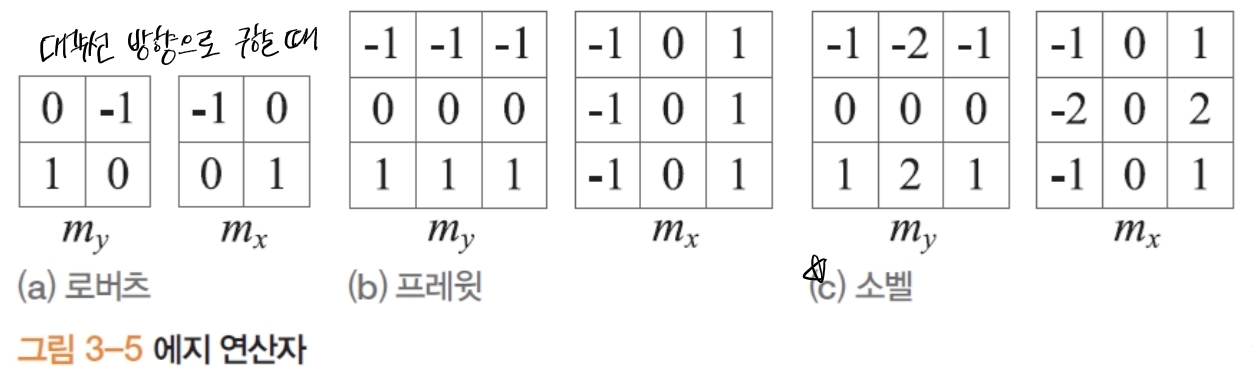
- Roberts: 매우 작은 2×2 대각 미분(노이즈 취약, 오래된 방식)
- Prewitt: 3×3, 미분 + 단순 평균 스무딩
- Sobel: 3×3, 중앙 가중 → Prewitt보다 스무딩 효과↑, $G_y=G_x^\top$
- Haar Filter: 가우시안 필터의 도함수
- 이진화 → Haar-like Filter: 사람 얼굴 99% 확률로 검출, 사람 얼굴 X 50% 확률로 검출
- 필터를 여러번 적용하자! → Ada Boost
- Haar-like Filter를 4번 적용: 사람 얼굴 약 95% 확률로 검출, 사람 얼굴 X 약 5% 확률로 검출
1.5. 에지 강도와 에지 방향
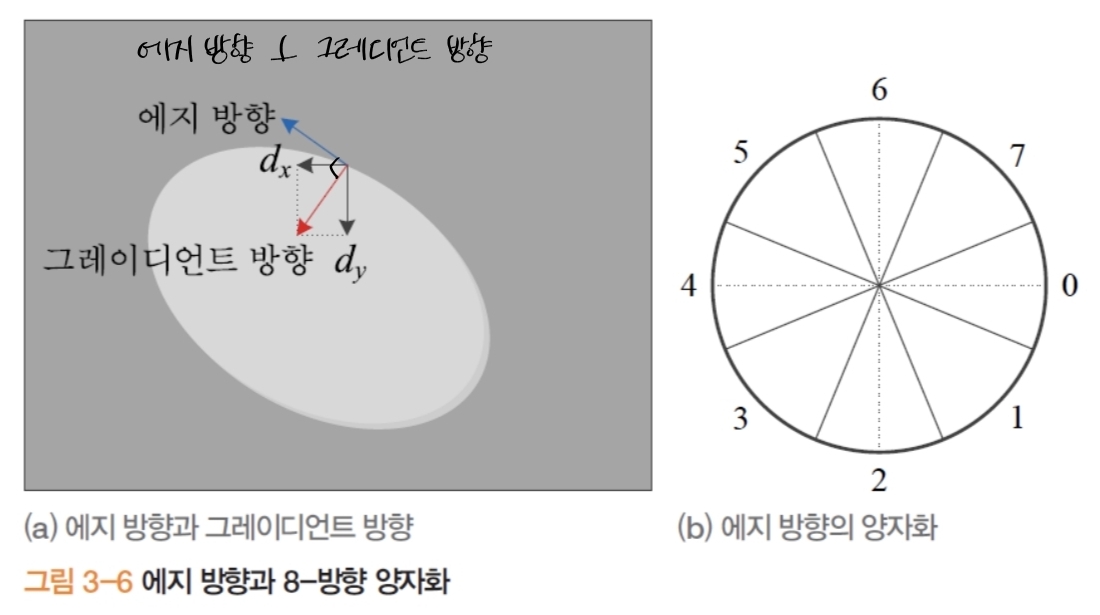
- 2D 그레이스케일 $I(x,y)$에서 기울기(gradient)
- gradient: \(\nabla f=(\frac{\partial f}{\partial y}, \frac{\partial f}{\partial x})=(d_y, d_x)\)
- 에지 강도: \(S(y, x) = \vert \nabla f \vert=\sqrt{d_y^2+d_x^2}\)
- gradient 방향: \(D(y, x) = \theta=\operatorname{arctan}(\frac{d_y}{d_x})\)
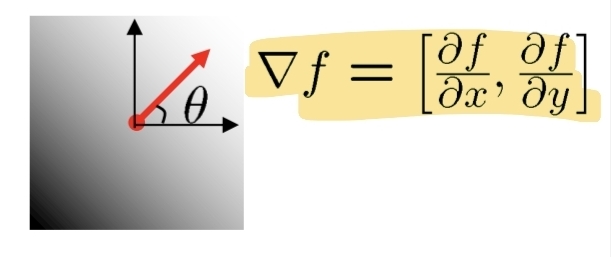
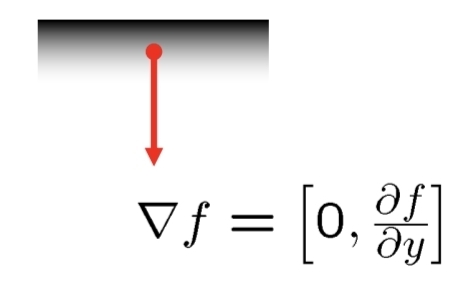
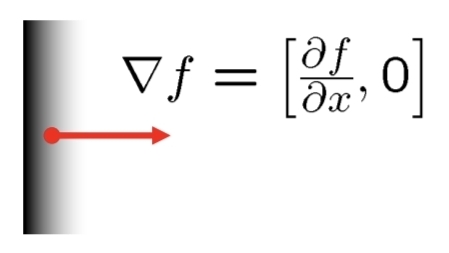
- 예제
2. 영(0)교차 이론
- 핵심 아이디어: 가우시안으로 스무딩 후 라플라시안 $\nabla^2$(2차 미분) 적용 → 0 교차 위치를 에지로.
- $\nabla^2 (G_\sigma * I) = (\nabla^2 G_\sigma) * I = LoG_\sigma * I$
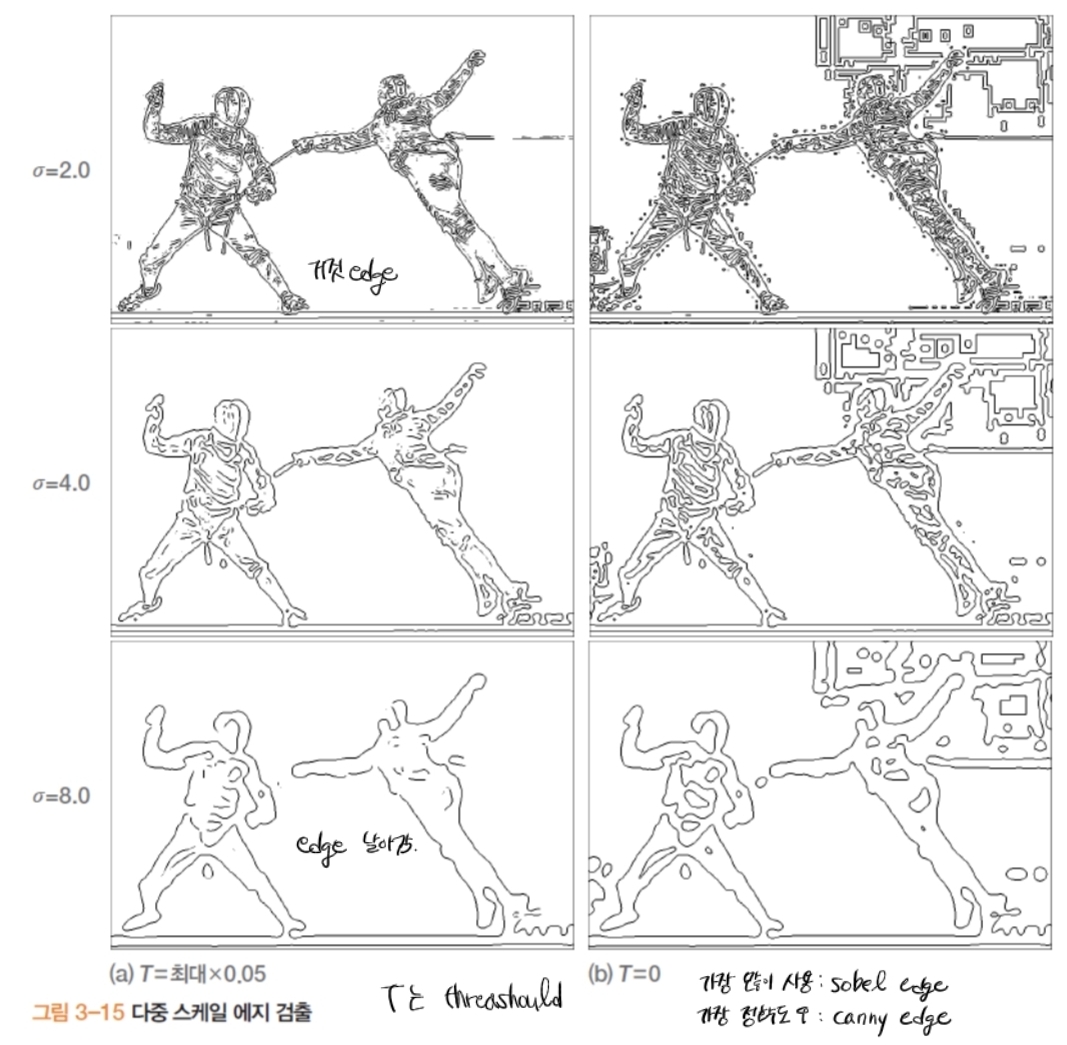
- 장점: 스케일 $\sigma$로 에지의 세밀도 조절, 얇고 닫힌 경계 추출 용이.
- 구현 팁
- LoG 직접 컨볼루션 또는 DoG(차분 가우시안) 로 근사.
- 제로 교차 판정 시, 이웃 픽셀 간 부호 변화와 2차 미분 크기 임계를 함께 사용해 잡음 억제.
2.1. 가우시안
2.1.1. 가우시안 사용 이유
- 미분은 잡음을 증폭 → 스무딩 적용
- 스케일 로 에지의 세밀도 조절
2.1.2. 가우시안 수식
- 1차원: \(G(x)=\frac{1}{\sqrt{2\pi}\,\sigma} e ^{-\frac{x^{2}}{2\sigma^{2}}}\)
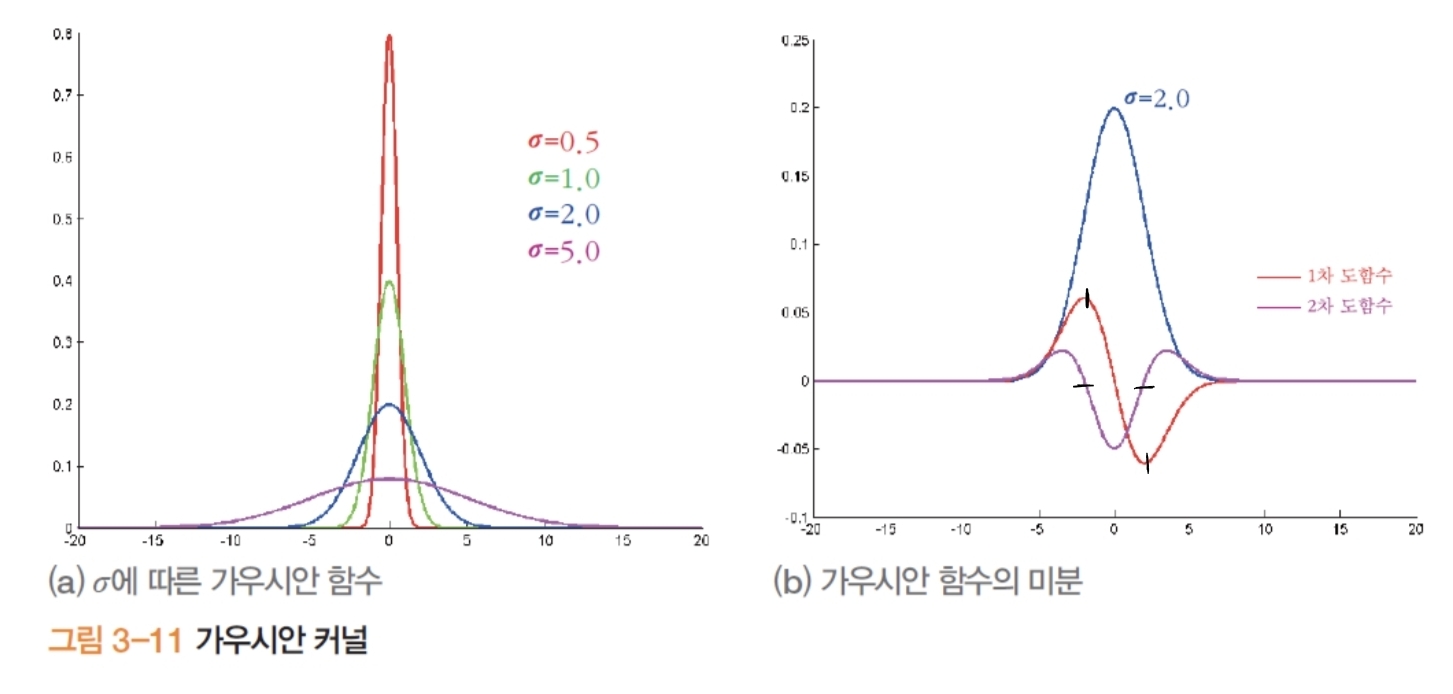
- 2차원: \(G(y,x)=\frac{1}{2\pi\sigma^{2}} e^{-\frac{y^{2}+x^{2}}{2\sigma^{2}}}\)
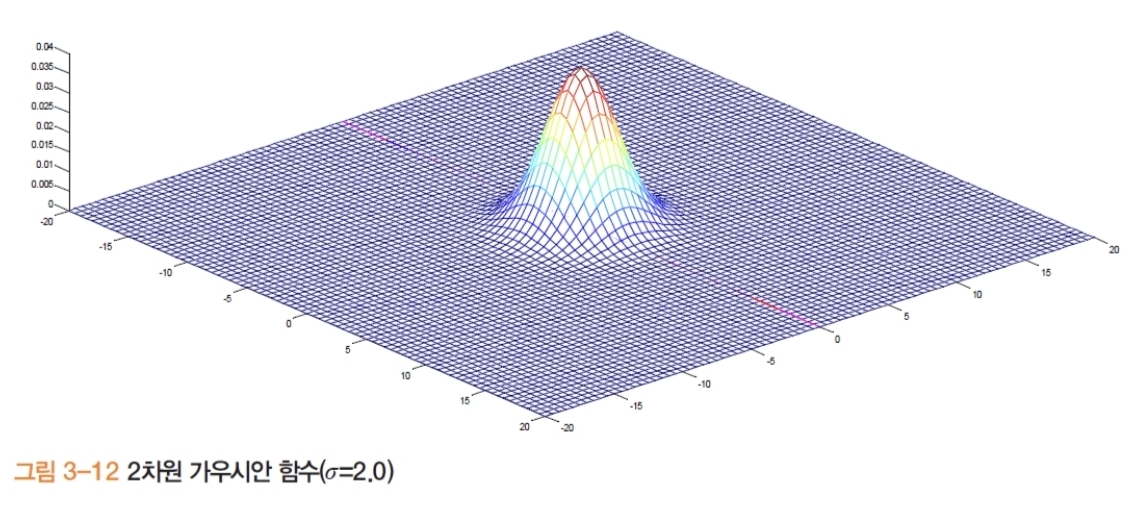
- 커널 크기: $\text{size} \approx 6\sigma+1$ (가장 작은 홀수) 권장
2.2. LOG 필터
- 2차 미분에서 영교차 검출
- \[\begin{align} \nabla^{2}f(y,x)&=\frac{\partial^{2}f}{\partial y^{2}}+\frac{\partial^{2}f}{\partial x^{2}} \\ &= \big(f(y{+}1,x)+f(y{-}1,x)-2f(y,x)\big) + \big(f(y,x{+}1)+f(y,x{-}1)-2f(y,x)\big) \\ &= f(y{+}1,x)+f(y{-}1,x)+f(y,x{+}1)+f(y,x{-}1)-4f(y,x) \end{align}\]
- LOG 필터: \(L=\begin{bmatrix} 0&1&0\\ 1&-4&1\\ 0&1&0 \end{bmatrix}\)
- Sharpening 필터: \(L=\begin{bmatrix} 0&-1&0\\ -1&4&-1\\ 0&-1&0 \end{bmatrix}\)
- LoG 필터: 입력 영상에 가우시안 G를 적용한 후, 결과에 라플라시안을 다시 적용하는 두 단계의 비효율성
- LoG (convolution:
*): \(\mathrm{LoG}(y,x)=\nabla^{2}\!\big(G(y,x)*f(y,x)\big) = \big(\nabla^{2}G(y,x)\big)*f(y,x)\) - 가우시안의 라플라시안: \(\nabla^{2}G(y,x)=\left(\frac{y^{2}+x^{2}-2\sigma^{2}}{\sigma^{4}}\right)G(y,x)\)


- LoG (convolution:
3. 컬러 에지
3.1. 채널별 처리의 한계
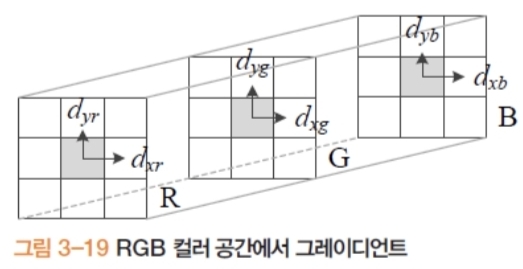

- RGB 각 채널에 독립 적용 후 OR 하면 채널마다 에지 위치가 달라 불일치/중복 발생.
3.2. 디 젠조(Di Zenzo) 접근
- 컬러(벡터) 기울기 성분 (채널 r,g,b): \(\begin{aligned} g_{yy} &= (d_{yr})^{2}+(d_{yg})^{2}+(d_{yb})^{2},\\ g_{xx} &= (d_{xr})^{2}+(d_{xg})^{2}+(d_{xb})^{2},\\ g_{yx} &= d_{yr}d_{xr}+d_{yg}d_{xg}+d_{yb}d_{xb}. \end{aligned}\)
- 기울기(주고유벡터) 방향: \(D(y,x)=\tfrac{1}{2}\,\arctan\!\left(\frac{2\,g_{yx}}{\,g_{xx}-g_{yy}\,}\right)\)
- 에지 강도(주고유값의 제곱근): \(S(y,x)=\sqrt{\tfrac{1}{2}\Big((g_{yy}+g_{xx}) +(g_{xx}-g_{yy})\cos\!\big(2D(y,x)\big) +2g_{yx}\sin\!\big(2D(y,x)\big)\Big)}\)



Comments